Introducción
La importancia de las diferencias entre regiones sobre el comportamiento del crecimiento económico hace prioritario que se definan estrategias de competitividad por parte de los gobiernos nacionales y regionales. A través del tiempo ha sido ampliamente reconocido el papel de la industria en la generación de valor agregado y en el posicionamiento de la economía nacional en los mercados internacionales. No obstante, dicho desempeño está condicionado al nivel de desarrollo y a las sinergias existentes en los mercados, entre otros factores.
Este estudio tiene como objetivos: a) cuantificar las diferencias en la evolución temporal de la productividad aproximada por medio del cálculo de la eficiencia técnica entre regiones y sectores, para Colombia durante las últimas dos décadas y b) identificar en qué medida las diferencias en el comportamiento de la evolución de la eficiencia responden a cambios en los patrones de especialización sectorial y la concentración (diversidad) de la actividad económica por sector o región en el tiempo, entre otros.
El estudio de la evolución y determinantes de la productividad en Colombia tiene larga trayectoria a nivel regional o sectorial; sin embargo, solo Iregui, Melo y Ramírez (2006) explotan las dimensiones regional y sectorial de manera simultánea, a partir de la estimación por efectos fijos. Desde el enfoque de fronteras estocásticas, Gallón (2007) y Loaiza y Franco (2012) comparan diferencias en la eficiencia regional por departamentos. Acevedo y Ramírez (2005) y Quintero, Prieto, Barrios y Leviller (2008) comparan diferencias en la eficiencia regional, en el primer caso para el sector textil y en el segundo para un conjunto de empresas de diversos sectores. La mayoría de estos estudios emplean la técnica de estimación de la eficiencia time varying propuesta por Battese y Coelli (1995), la cual supone que el comportamiento temporal de la eficiencia sigue una tendencia y que esta es común a todos los individuos. Sin embargo, este supuesto es bastante restrictivo si se analizan grupos de individuos heterogéneos o si se emplean series de tiempo largas, donde el patrón temporal puede variar entre individuos o en el tiempo. Algunos, incluso, omiten la importancia de considerar las diferencias sectoriales en los coeficientes tecnológicos, para el cálculo consistente de la productividad.
Este estudio aproxima la evolución y principales diferencias regionales en la productividad por sectores para la industria colombiana durante el periodo 1992-2010, con datos de la Encuesta Anual Manufacturera (EAM) para nueve áreas metropolitanas y sectores de actividad (CIIU a dos dígitos). El cálculo de la productividad se hace aplicando técnicas de fronteras estocásticas time varying que no imponen supuestos rígidos al patrón de evolución temporal entre individuos. Además, se propone un análisis de descomposición dinámico de la varianza de la eficiencia técnica predicha, que permite indagar sobre la importancia relativa de los procesos de especialización sectorial, la concentración regional de la industria, la concentración sectorial en determinadas regiones o cambios en la composición sectorial de la industria, en las diferencias en la evolución individual de la eficiencia técnica de los sectores y las regiones, para un periodo bastante dilatado. Este último constituye un aporte tanto a la literatura nacional como internacional sobre el tema y los resultados obtenidos van en línea con estudios en el ámbito internacional que emplean otras metodologías (Glaeser, Kallal, Scheinkman y Schleifer, 1992; Henderson, Kuncoro y Turner, 1992; Melo, Graham y Noland, 2009; Puga, 2010; Rosenthal y Strange, 2004, entre otros).
Los resultados evidencian un fortalecimiento industrial de las principales ciudades del país y una profundización en el rezago del resto. La competitividad sectorial de las regiones está positivamente correlacionada con su nivel de especialización. El análisis de descomposición de la varianza de la eficiencia técnica presentó una correlación positiva entre cambios en la eficiencia promedio y ganancias por reasignación de recursos, más fuerte a nivel regional. La descomposición dinámica de la varianza de la eficiencia técnica mostró que el proceso de reasignación de recursos ha estado liderado por procesos de profundización en la especialización sectorial y de concentración regional o sectorial de la actividad económica. Es importante fortalecer la dotación regional de capital físico y humano, entre otros factores que favorecen la competitividad, y definir estrategias con base en sectores líderes para impulsar el desarrollo industrial de las regiones. Este documento se compone de una revisión de literatura, la metodología de estimación, los resultados econométricos y la descomposición de la varianza de la eficiencia técnica. Y por último, de las conclusiones.
I. Revisión de literatura
En Colombia es amplia la tradición de estudios que intentan aproximar y explicar el comportamiento de la productividad en términos agregados y sectoriales. Las propuestas con carácter agregado normalmente emplean medidas de la productividad multifactorial (PM) y la productividad del trabajo (PT), para indagar sobre las consecuencias de la apertura económica y la relación con mercados extranjeros (Clavijo, 1990, 1991, 2003; Echavarría, 1990; García, 1988).
En el grupo de trabajos compilados por Chica se trata de indagar sobre los determinantes de la productividad (Chica, 1996; Ramírez y Jaramillo, 1996; Sánchez, Rodríguez y Núñez, 1996), o se presentan análisis para sectores específicos: Bonilla (1996) para bienes de capital, Cárdenas (1996) para petroquímica y plásticos, Corchuelo (1996) para papel e imprentas y Zuleta (1996) para textil y confecciones. La propuesta más reciente de Meléndez, Medina y Kassem (2002) aporta datos de empresas para el sector alimenticio.
La Encuesta Anual Manufacturera (EAM) ha sido la principal fuente de análisis sectorial. Existen estudios con datos agregados por sectores que indagan sobre el comportamiento dinámico de la productividad (Bonilla, 2000; Pombo, 1999), la importancia del capital público o del capital humano (Cárdenas, Escobar y Gutiérrez, 1995; Jiménez y Sanau, 2011; Sánchez et al., 1996); o, con datos de empresas, sobre los efectos de la apertura económica y las reformas de los años ochenta y noventa2 sobre la productividad y la asignación de recursos (Eslava, Haltiwanger, Kugler y Kugler, 2004; Fernandes, 2007; Meléndez, Seim y Medina, 2003), o sobre su relación con el capital extranjero y la innovación (Echavarría, Arbeláez y Rosales, 2006; Sandoval, 1982). Referencias que aborden las diferencias regionales en productividad son más escasas. Se identificaron los estudios de Cárdenas et al. (1995) e Iregui et al. (2006). No obstante, Iregui et al. son los únicos que tratan de explotar las dimensiones sectorial y regional a la vez (a través del enfoque de efectos fijos).
La metodología de fronteras estocásticas es ampliamente utilizada a nivel internacional para el análisis de la productividad y las diferencias en eficiencia3. En Colombia no ha sido muy empleada. Para el análisis de la industria, se identificaron los trabajos de Acevedo y Ramírez (2005), que analizan si las diferencias regionales en el sector textil pueden ser explicadas por la concentración industrial, y Quintero et al. (2008), que comparan la productividad entre regiones, a partir de información de la Superintendencia de Sociedades y encuentran que las empresas de Cartagena son las más eficientes del país. Gallón (2007) y Loaiza y Franco (2012) realizan una descomposición del crecimiento de la productividad por departamentos. Loaiza y Franco (2012) además relacionan esta medida con el índice de especialización, el peso de las exportaciones y el peso de las importaciones, y encuentran un efecto positivo en el primero y negativo para los dos últimos. No obstante, la mayoría de estos estudios emplean la técnica de estimación de la eficiencia time varying propuesta por Battese y Coelli (1995)4, la cual supone que el comportamiento temporal de la eficiencia sigue una tendencia y que esta es común a todos los individuos, lo que puede ser bastante restrictivo. Además, no considerar las diferencias tecnológicas intersectoriales puede sesgar el análisis. Se recomienda comparar de un modo intrasectorial, para evaluar individuos relativamente homogéneos.
Por otra parte, en la literatura internacional existe un amplio consenso sobre la importancia de las economías de aglomeración entre otras externalidades y de los procesos de especialización y concentración (diversidad) sectorial sobre el crecimiento económico (Glaeser et al., 1992; Henderson et al., 1992; Melo et al., 2009; Puga, 2010; Rosenthal y Strange, 2004).
II. Estimación de la productividad a partir de fronteras estocásticas time varying
El papel central que desempeñan el crecimiento económico y las diferencias regionales en el diseño de la política pública han hecho de este uno de los campos más prolíferos de las últimas décadas. A pesar de que la estimación de la productividad total de los factores (PTF) sigue siendo el centro de atención metodológica, la aparición de más y mejores datos y de nuevas técnicas estadísticas y econométricas desde otros enfoques5 le han permitido ganar robustez al análisis, flexibilizar los supuestos teóricos de partida y aportar conclusiones de política más cercanas a la realidad de los países.
Las metodologías más comunes empleadas para aproximar el cálculo de la PTF van desde las técnicas no paramétricas, como los números índices, hasta las técnicas paramétricas para estimar funciones de producción con distintas especificaciones tecnológicas y, más recientemente, el uso de fronteras estocásticas de producción para calcular la ratio de eficiencia técnica. Véase Gallón (2007) para una comparación de las debilidades y fortalezas desde el punto de vista teórico de las diferentes alternativas existentes.
La estimación de fronteras estocásticas de producción fue propuesta por Aigner, Lovell y Schmidt (1977) y Meeusen y Van den Broeck (1977), y surgió como una metodología alternativa que permite obtener un indicador sintético acotado entre 0 y 1, para cuantificar la diferencia en “productividad” entre individuos heteroéneos que realizan una asignación diversa de los recursos, suponiendo que la tecnología es similar para todos y que, por tanto, existe un “individuo representativo”, cuya producción se podría ubicar sobre la frontera de posibilidades de producción.
La metodología de fronteras estocásticas se definió para analizar de qué manera las decisiones de individuos heterogéneos, como establecimientos o empresas, afectan la eficiencia relativa. Sin embargo, las restricciones en la disponibilidad de información microeconómica común en muchos países han trasladado su aplicación al análisis de datos agregados para regiones, países, sectores, etc. Trasladar el análisis a datos agregados tiene la limitación de ocultar la heterogeneidad individual y presentar un “resumen del efecto neto entre ganadores y perdedores” en función de la productividad. Al respecto, Balk (2003) analiza los resultados obtenidos con datos agregados y microeconómicos y concluye que, a pesar de la limitación inherente de trabajar con datos agregados, estos pueden interpretarse como el comportamiento de un “superindividuo” al comparar su desempeño respecto a un nivel superior, y que lo que realmente importa como soporte para el análisis de la productividad es la calidad de la información y la representatividad que esta tiene dentro de la población.
La tecnología de producción del individuo i se expresa en términos lineales como:
donde Yi es el nivel de producción del individuo i, f (Xi, β) es el componente explicado por la combinación de insumos productivos utilizados en la producción por el individuo i, ei es el componente explicado por factores no observables o aleatorios que afectan el nivel de producción observada.
El enfoque de fronteras estocásticas, supone que el término de error (ei) en realidad tiene dos componentes, uno propiamente aleatorio o estocástico (vi) y otro que recoge la “ineficiencia productiva” (ui).
En este sentido, si ei = vi + ui, la ecuación (1) se puede reexpresar, como:
donde Yif representa el nivel de producción frontera para el individuo i, por lo cual:
Si ui = 0, indica que el individuo tiene 0 nivel de ineficiencia, lo que es coincidente con el nivel de producción en la frontera estocástica (Yif = Yi).
Si ui > 0, representa en qué medida la producción observada para el individuo i se aleja de la producción frontera. A mayor valor de ui, es mayor el nivel de ineficiencia (Yif > Yi). Entonces, la ratio de eficiencia técnica (ETi) se define como:
Dado que ui es inobservable, la estimación de la eficiencia técnica (ETi) se obtiene a partir de su distribución condicionada respecto al término de error ei, como E[ui |ei]. Normalmente, esta descomposición se realiza aplicando técnicas de máxima verosimilitud, para las cuales es necesario presuponer que el término de ineficiencia ui sigue una distribución estadística conocida6. Véanse Kumbhakar y Lovell (2000) para un estudio bastante completo sobre los aspectos metodológicos y los enfoques desarrollados respecto a la estimación de fronteras estocásticas.
Cuando se dispone de información tipo panel, la estimación de fronteras estocásticas permite predecir la eficiencia time invarianto time varying. Las técnicas time invariant son útiles para identificar las diferencias en eficiencia técnica entre individuos, sin necesidad de imponer a priori supuestos distribucionales sobre el término de eficiencia. No obstante, cuando el espacio temporal es amplio, es irrealista suponer que el término de eficiencia se mantiene constante. Las técnicas time varying surgen como una alternativa que permite modelar el patrón temporal de la eficiencia; sin embargo, la mayoría de las propuestas imponen patrones temporales rígidos u homogéneos para todos los individuos, lo cual tampoco parece ser muy realista7, o son muy demandantes en recursos8. Como principales exponentes de estas metodologías, se encuentran:
Time invariant:
– Schmidt y Sickles (1984): efectos fijos.
– Pitt y Lee (1981): efectos aleatorios-máxima verosimilitud.
Time varying:
– Cornwell, Schmidt y Sickles (1990): tendencia cuadrática,
– Lee y Schmidt (1993):
con dummies temporales.– Kumbhakar y Hjalmarsson (1993):
a partir de una estimación en dos etapas, método de momentos.– Greene (2005): true fixed effect (TFE) y true random effects (TRE).
La propuesta de Kumbhakar y Hjalmarsson (1993) permite obtener una medida de ineficiencia que cambia libremente en el tiempo para cada individuo, lo cual es ideal para modelar la dinámica temporal ante muestras de población heterogénea y, en este caso, muy adecuado para el análisis de sectores como la industria, que han presentado cambios significativos en los últimos años, a nivel mundial. En este estudio, se aplicará una versión de esta metodología, propuesta en Raymond, Roig, García y Gómez (2010), la cual utiliza técnicas de máxima verosimilitud en lugar del método de momentos9.
La adaptación de la metodología en dos etapas a la estimación de la eficiencia técnica al panel de tres dimensiones (sector, región y tiempo) requiere consideraciones especiales por la naturaleza de los datos10. Los “sectores” se asumen como unidad de referencia y análisis, y dentro de ellos, se buscará identificar las diferencias entre regiones y su patrón de evolución temporal. Las etapas por desarrollar son:
1) En la primera etapa, se estima paramétricamente la función de producción suponiendo una tecnología tipo Cobb Douglas y efectos fijos:
donde yit es el logaritmo del valor agregado del individuo i en el periodo t; kit es el logaritmo del capital; nit es el logaritmo del empleo; β0 es el logaritmo de la PTF común a todos los individuos en el tiempo; βk y βn, las elasticidades del capital y del empleo, respectivamente. Los subíndices, corresponden a los j-sectores, ∀ j = 1,…9; i-regiones, ∀ i = 1,…9; y t-periodos, ∀ t = 1992,…, 2010. Así, μi es el efecto fijo de la región i en el sector j y zit es el término de error aleatorio que capta factores inobservables o estocásticos, que afectan el nivel de valor agregado de la región i en el sector j, para el año t.
De acuerdo con la ecuación (5), estimar un único modelo por efectos fijos para toda la muestra es equivalente a suponer que la tecnología de producción es idéntica para todos los sectores de actividad; es decir, que las elasticidades del capital y del empleo son constantes entre sectores, lo cual parece poco realista. Para superar esta posible limitación, se opta por estimar un sistema de ecuaciones aparentemente no relacionadas (seemingly unrelated regressions, SURE), por sector de actividad (∀ j = 1,…9):
Esta metodología evita suponer una tecnología homogénea entre sectores de actividad, dado que permite la estimación de ecuaciones separadas y posibilita ganancias de eficiencia explotando las covarianzas no nulas entre las perturbaciones aleatorias (zjit) de las distintas ecuaciones (Zellner, 1962). La estimación por SURE requiere el cumplimiento del supuesto de exogeneidad contemporánea, en este caso, para cada sector de actividad (Cameron y Trivedi, 2008). No obstante, la estimación de los coeficientes tecnológicos en una función de producción normalmente está expuesta a problemas de endogeneidad. La inclusión de efectos fijos de región para cada sector (μji) corrige la endogeneidad asociada al componente de productividad time invariant. Pero la imposibilidad de controlar en el modelo otras variables como la capacidad de utilización y la posible correlación existente entre el nivel de utilización de insumos productivos y la productividad inobservada time varying, o la correlación serial del término de error, hace que sea necesario considerar medidas alternativas para su corrección, con el fin de obtener estimadores consistentes y robustos.
Stock y Watson (1993) desarrollaron el método de mínimos cuadrados ordinarios dinámicos (dynamic ordinary least squares, DOLS), que consiste en estimar por MCO una regresión ampliada que incluye, además, los valores futuros (t + 1), contemporáneos (t) y pasados (t− 1), de las primeras diferencias de las variables explicativas consideradas en el modelo, con el fin de controlar por problemas de endogeneidad y obtener errores estándar robustos a la correlación serial de largo plazo. Además, en el caso de series temporales crecientes, es necesario verificar si se trata de series integradas y, de ser así, si los procesos están cointegrados. Para contrastar la validez de la inferencia realizada, se aplicarán las pruebas de integración y cointegración para datos tipo panel.
2) En la segunda etapa, se predice el pseudoerror para cada sector, a partir de la estimación del sistema propuesto en la ecuación (6), como:
La estimación de fronteras estocásticas presupone que la tecnología de producción es comparable entre individuos, para que tenga sentido el cálculo y posterior interpretación de la eficiencia técnica (acotada entre 0 y 1). Por esta razón, el componente de ineficiencia técnica (ujit) de cada región en el tiempo se aproximará a partir de regresiones separadas para cada sector j, estimadas por máxima verosimilitud. De esta manera, la unidad homogénea es el sector y dentro de él se puede identificar qué regiones son más o menos eficientes y cómo ha sido la evolución de este indicador en el tiempo. Siguiendo esta metodología, el término de ineficiencia time varying (ujit) no está condicionado a seguir un patrón fijo, ni homogéneo, entre individuos. Es necesario comparar entre modelos alternativos que corrigen por heterocedasticidad en u o v, para dar mayor robustez a los resultados11. Una vez predicho el valor de la ineficiencia técnica (u), se calcula la ratio de eficiencia técnica (ET), como:
La eficiencia técnica para los agregados de región, sector y total se construye como una media ponderada de la eficiencia técnica predicha para cada individuo, representado por las regiones, los sectores, o las regiones y sectores:
donde ETjit es la eficiencia técnica predicha para la región i en el sector j, en el año t; pjit es la participación del empleo de la región i en el sector j, en el total de la industria para el año t; pjt1 es la participación del empleo del sector j en el año t, para la región I, con I = 1,…,9; pitj es la participación del empleo de la región i en el año t, para el sector J, con J = 1,…,9. Las mayúsculas en los superíndices indican que el nivel de análisis se mantiene constante para cada región I o sector J (es decir, la participación suma 1 en I o en J).
III. Estimación de la eficiencia técnica time varying
Se empleó la información de la EAM12 realizada por el Departamento Administrativo Nacional de Estadística (DANE), para el periodo 1992-2010. El análisis se realizó para nueve áreas metropolitanas13 y nueve sectores de la industria14 (clasificación CIIU a dos dígitos)15. Se conformó un panel balanceado de nueve regiones, nueve sectores y 19 años, para un total de 1.539 observaciones. Se partió de una función de producción de tipo Cobb-Douglas con rendimientos constantes a escala (βn = 1 − βk)16. La variable dependiente es el valor agregado (yjit)17. El empleo (njit) corresponde al personal ocupado total. No fue posible corregir la variable empleo, por capital humano, dado que la clasificación por nivel educativo no es homogénea para todo el periodo. El capital (kjit) se calculó como la suma del capital en: mq. y eq. industrial, mq. y eq. de transporte, mq. y eq. de oficina, y en edificios y estructuras, calculados a partir de inventario permanente18. Se tomó el valor de los activos en el año anterior como valor inicial del capital. Se deflactó con el índice de precios al productor (IPP, 1994 = 100), por sector CIIU tres dígitos; fuente: Banco de la República-DANE.
Dada la naturaleza de los datos, es necesario verificar si las series son estacionarias o no. Los contrastes usuales de raíces unitarias parten del supuesto de independencia cross section y la violación de este supuesto puede sesgar las conclusiones obtenidas. Se contrastó la hipótesis de independencia individual para datos panel a partir de Pesaran (2004), y esta resultó rechazada. Por tanto, se contrastó la hipótesis de raíz unitaria a partir de Pesaran (2007) (CIPS), que permite controlar por dependencia cross section. Esta prueba, al igual que en Im, Pesaran y Shin (2003), es decir, IPS, es una prueba tipo ADF que permite heterogeneidad individual en la hipótesis alternativa (Ha) y es flexible en la modelación de la estructura de rezagos para cada individuo, sin embargo, no está sujeta a N < T19. El cuadro 1 recoge los resultados. Se rechaza la hipótesis nula de raíz unitaria para todas las variables, a favor de la evidencia de procesos estacionarios en tendencia20, con deriva, o con patrón autorregresivo, y dependencia cross section21. La baja potencia del test de raíces unitarias permite confiar en caso de rechazar la hipótesis nula (Ho).
Cuadro 1.
Prueba de raíces unitarias con dependencia entre individuos
| Variable | Ln(VA) | Ln(Empleo) | Ln(Capital) |
| CIPS* | -4,37 | -3,19 | -4,10 |
| Decisión | Rechazar | Rechazar | Rechazar |
Los cuadros 2 y 3 recogen los resultados de los modelos estimados. El cuadro 2 presenta la estimación por efectos fijos (least squares dummy variable, LSDV), para el conjunto de la muestra. Dado que no se excluye ningún subsector, la elasticidad del capital en este caso representa el valor para el conjunto de la industria. Este cuadro presenta cuatro estimaciones: corrigiendo y sin corregir posibles problemas de endogeneidad y autocorrelación serial a partir de DOLS y estas estimaciones, a su vez, corrigiendo y sin corregir por heterocedasticidad individual, con lo que se obtienen errores estándar robustos a la presencia de clúster por región22.
Cuadro 2.
Estimación modelo conjunto para la industria colombiana por efectos fijos de sector y región: 1992-2010
| LSDV - sin DOLS | LSDV - con DOLS | |||
| Variable | (1) | (2) | (3) | (4) |
| 0,301a | 0,301 | 0,303 | 0,303 | |
| L(K/N) | 0,014b | 0,041 | 0,020 | 0,047 |
| 22,0c | 7,4 | 15,1 | 6,5 | |
| 7,30 | 7,30 | 7,31 | 7,31 | |
| Constante | 0,139 | 0,414 | 0,206 | 0,477 |
| 52,6 | 17,6 | 35,5 | 15,3 | |
| FE (región y sector) | Sí | Sí | Sí | Sí |
| Errores estándar Robustos clúster área | No | Sí | No | Sí |
| N° obs. | 1.539 | 1.539 | 1.296 | 1.296 |
| N° individuos | 81 | 81 | 81 | 81 |
| N° años | 19 | 19 | 16 | 16 |
| Desv. est. error | 0,22 | 0,314 | 0,313 | 0,303 |
| R2 | 25,0% | 25,0% | 16,9% | 16,9% |
| Log verosimilitud | -398,3 | -398,3 | -289,3 | -289,3 |
| SC | 811,3 | 804,0 | 614,5 | 607,3 |
| AIC | 800,7 | 798,7 | 588,7 | 586,7 |
| Ho: Todos ui = 0: | F = 32,35 Prob > F = 0,0000 | F = 28,96 Prob > F = 0,0000 | ||
Las cuatro estimaciones arrojan resultados bastante similares. En primer lugar, corregir o no corregir la endogeneidad por DOLS no cambia los resultados de manera significativa, lo que sugiere que a nivel agregado el problema de endogeneidad no es tan fuerte, después de controlar por efectos fijos de región y sector. Según el modelo (4), del cuadro 2, la elasticidad del capital es de 0,303, lo que implica una elasticidad del empleo cercana a 0,70 (resultado en línea con otros estudios para el caso colombiano). La corrección de heterocedasticidad robusta a la presencia de clúster por región triplicó el valor de las desviaciones estándar, pero a pesar de ello, las variables continúan siendo estadísticamente significativas23.
Estudios para Colombia, que han empleado técnicas no paramétricas para la estimación de la productividad, han tomado ponderaciones del capital cercanas al 0,30 (Sánchez et al., 1996 emplean 0,37 para el periodo 1950-1994 y Pombo, 1999 emplea 0,33 para 1970-1995). A partir de estimaciones con técnicas paramétricas, Eslava et al. (2004) encuentran una elasticidad de 0,32 para el capital y de 0,74 para empleo, respecto al valor agregado24, para el periodo 1977-1999.
Es importante aclarar que el estudio de Eslava et al. (2004) introduce corrección por capital humano y por capacidad de utilización a partir de los datos de empresas de la EAM. Se esperaría que dicha corrección ajuste al alza el peso del capital físico y humano. A pesar de no aplicar esta corrección, nuestros resultados son bastante similares a los suyos. Además, si se comparan las diferencias entre periodos de análisis, parece que el peso del capital se ha reducido paulatinamente, lo cual no es extraño, ya que el empleo con mayor nivel de cualificación ha ganado importancia en la industria mundial.
El único estudio directamente comparable con nuestros datos es el de Iregui et al. (2006). Ellos obtienen una elasticidad del capital de 0,15, lo cual pareciera ser muy bajo de acuerdo con la literatura. Los autores sugieren como explicación la exclusión de algunos subsectores. Sin embargo, como se puede observar en el cuadro 3, la elasticidad del capital entre sectores no difiere de manera muy significativa, resultado soportado por la evidencia sectorial presentada por otros autores (Cárdenas et al., 1995; Jiménez y Sanau, 2011; Meléndez et al., 2003). Este estudio realizó una comparación entre metodologías alternativas para el cálculo del capital, entre las cuales se incluyó la empleada por Iregui et al. (2006). Pareciera que el procedimiento empleado por ellos para el cálculo de la variable inversión puede subestimar su verdadero valor (véase anexo 3).
El cuadro 3 presenta los resultados de la estimación por sector de actividad a través de SURE. Los cuadros 3A y 3B presentan la comparación de resultados respecto a no corregir versus corregir por DOLS. Las regresiones sectoriales presentan mayor ajuste en los coeficientes estimados de la elasticidad del capital al corregir por DOLS (respecto a la estimación agregada), lo que indica que los problemas de endogeneidad pueden afectar en mayor medida la inferencia, si no son tenidos en cuenta. En ambos casos, el test de Breusch-Pagan rechaza la hipótesis nula de independencia entre ecuaciones del sistema, lo cual valida la estimación por la vía de SURE, frente a realizar estimaciones separadas por MCO. Los efectos fijos individuales de región resultaron conjuntamente significativos en todos los casos. Las estimaciones sectoriales de la elasticidad del capital coinciden en alto grado con las presentadas por otros estudios, sobre todo con Jiménez y Sanau (2011), que emplean CIIU a dos dígitos, lo cual pareciera ser evidencia de consistencia en los resultados presentados y valida la inferencia derivada de estos.
De acuerdo con las estimaciones del cuadro 3B, los sectores con mayor intensidad del capital son: otras manufacturas, alimentación, caucho y bienes de capital, con elasticidades capital de 0,53, 0,34, 0,33 y 0,32, respectivamente. Los sectores que resultaron más intensivos en trabajo fueron: papel, metalurgia, química y textil, con elasticidades capital de 0,178, 0,183, 0,23 y 0,25, respectivamente. A partir de la estimación de los coeficientes tecnológicos por sector, en la segunda etapa se procede a estimar el componente de ineficiencia técnica time varying.
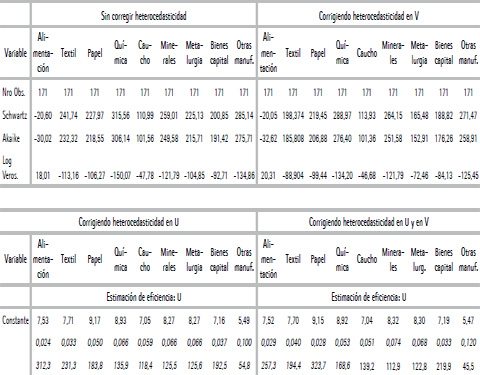
El cuadro 4 presenta los resultados del modelo empleado para predecir la ineficiencia técnica para cada uno de los sectores j, que fueron elegidos a partir de los criterios de Akaike y Schwartz entre modelos alternativos que corrigen por heterocedasticidad en u y/o en v25. Para todos los sectores se rechazó la hipótesis de homocedasticidad en el término de ineficiencia técnica (u). Esto implica que sería un grave error emplear técnicas time varying, que no permitan el control por heterocedasticidad, dado que se pueden distorsionar las conclusiones obtenidas. La mayoría de sectores presentaron además heterocedasticidad en el componente estocástico (v)26. A partir del cuadro 4, se procede a predecir el valor de la ineficiencia técnica (u) y a calcular el coeficiente de eficiencia técnica (ETJit) y sus valores ponderados por región, sector y agregado.
Notas: a coeficientes, b desviacion estandar, c estadisticos t.
Fuente: cálculos propios a partir de la EAM.
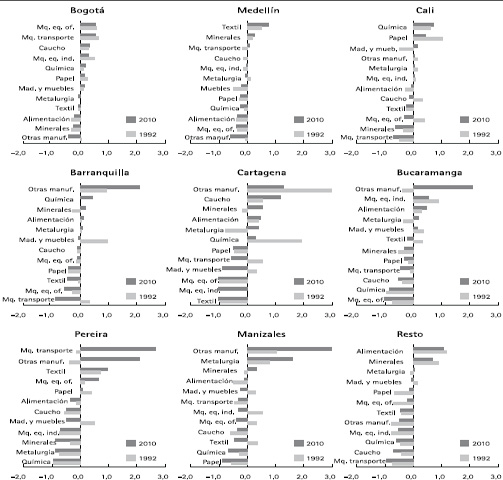
El gráfico 1 muestra que el sector con mayor nivel de eficiencia promedio para el periodo de estudio fue el de bienes de capital, seguido por metalurgia, caucho y alimentación. Los sectores con menor eficiencia promedio fueron papel, química y textil. Respecto a las diferencias regionales, Medellín es la región más eficiente en promedio, seguida por Bogotá y Cali. Pereira, Cartagena y Manizales son las menos eficientes.
Al analizar la eficiencia relativa de las regiones, por sector de actividad, se identifican ciertos patrones. Medellín resulta ser la región más eficiente en la producción textil, alimentación y otras manufacturas; Bogotá lo es en bienes de capital y es la segunda en textil. Cartagena, resto y Cali parecieran evidenciar ciertos eslabonamientos en química, caucho y minerales. Pereira, a su vez, parece ser la más eficiente en el sector papelero. La eficiencia técnica y el índice de especialización sectorial presentan una correlación del 24,8%27, lo que soporta la evidencia encontrada por Acevedo y Ramírez (2005).
Los paneles A y B del gráfico 2 recogen la evolución temporal de la eficiencia técnica para las regiones y los sectores, respectivamente. En ellos se puede observar el valor predicho de la eficiencia, la tendencia suavizada a través del filtro de Hodrick y Prescott y el crecimiento acumulado a partir del índice 1992 = 1,00 (izquierda a derecha). Las diferencias en la dinámica individual se hacen evidentes. Se confirma que los sectores textil y papelero han sido los más dinámicos durante los últimos veinte años. El sector de minerales aumentó sus niveles de eficiencia, sobre todo durante la primera década del siglo XXI. El sector textil fue uno de los sectores que más pudo aprovechar el proceso de apertura económica de los años noventa. Sin embargo, según la caída que muestra en 2006, parece haber sido afectado por la incertidumbre ante la negociación del tratado de libre comercio con Estados Unidos, principal mercado de sus exportaciones. El sector minero ha tenido un fuerte impulso por la entrada de inversión extranjera directa durante la primera década del siglo XXI.
Respecto al análisis por región, Bucaramanga es la que presentó un mayor aumento en los niveles de eficiencia en las últimas dos décadas (27% acumulado). La siguen en dinamismo Medellín (17,4%) y Bogotá (14,9%). En cambio, Cartagena pierde hasta un 19% en los niveles de eficiencia, siendo la región con peor balance. Barranquilla, a pesar de perder un 7,4% durante la década
Cuadro 4.
Estimación de fronteras estocásticas time varying
Notas: los valores están ordenados en orden descendente. El valor de cada región corresponde al promedio registrado entre 1992 y 2010.
Diferencia porcentual calculada a partir de índice con ref. industria = 100, Colombia = 100.
Fuente: cálculos propios a partir de la EAM.
Fuente: cálculos propios a partir de la EAM.
de los noventa, logra acumular un 3,7% de crecimiento acumulado durante el siglo XXI, lo cual indica una mejora en su situación en los últimos años.
El desempeño de Bucaramanga en las últimas décadas es muy superior a la media y sería interesante analizar qué fenómenos económicos están detrás de dicho comportamiento. Medellín es la ciudad que en las últimas dos décadas más apostó en inversión en infraestructura vial y social, lo que seguramente ha tenido fuerte impacto sobre su competitividad. Bogotá sin duda concentra la mayor cantidad de mano de obra cualificada como ciudad capital y es capaz en sí misma de atraer sectores altamente tecnológicos, lo que aumenta su ventaja competitiva. El comportamiento regional presentado en este apartado refuerza la hipótesis de divergencia o polarización sustentada por Bonet y Meisel (1999) y Galvis y Meisel (2012).
IV. Análisis de la descomposición de varianza de la eficiencia técnica
Con el fin de analizar el impacto de los procesos de relocalización y reasignación de la actividad productiva sobre la evolución de la eficiencia técnica, se plantea aplicar la descomposición de la productividad propuesta por Olley y Pakes (1996). Por otra parte, dado que la EAM es una encuesta censal para la industria, es posible asociar la participación del empleo (pjit) con la probabilidad de participar del sector j en la región i, en el periodo t, para la industria colombiana. Ello permite analizar la descomposición de varianza a distintos niveles de agregación (regional: R, sectorial: S, total: T), aplicando las leyes de la probabilidad. Tomando la ecuación (9), según Olley y Pakes (1996) se define:
donde ETitR y ETjtS es la media ponderada y 
es la media aritmética, de la eficiencia técnica de la región i, o el sector j, respectivamente, en el periodo t; 
es la probabilidad condicionada (PC) del sector j, en la región I, con I=1,…,9, en t, es decir, la composición sectorial de las regiones; 
es la probabilidad condicionada (PC) de la región i, en el sector J, con J=1…,9, en t, es decir, la composición regional de los sectores.
Las ecuaciones (10) y (11) descomponen la ET regional y sectorial en dos:
ganancia en eficiencia media para todos los individuos (en R o S)
ganancia por reasignación de recursos 
implica que la media pondera en mayor medida las desviaciones positivas (los sectores más eficientes tienen mayor peso).
El cuadro 5 presenta los resultados de esta descomposición. En primer lugar, existe una ganancia en eficiencia por reasignación de recursos para el conjunto de la industria durante las dos décadas (0,055 y 0,046, respectivamente). No obstante, a nivel regional y sectorial se observa una alta heterogeneidad. Cali y Barranquilla presentan una reasignación negativa promedio durante el periodo de estudio, lo que implica un menor peso de sectores más eficientes en la región. Las demás regiones presentan una reasignación positiva. Todos los sectores presentan una reasignación positiva. Es decir, los sectores tienen mayor peso en las regiones más eficientes, siendo este efecto más importante para textil, química y papel.
El gráfico 3 compara las diferencias entre décadas en la ganancia a través del aumento de la eficiencia promedio 
versus la ganancia por reasignación de recursos 
.28 Se definen como ganadores netos quienes se posicionan en el cuadrante superior derecho, dado que logran aumentar su eficiencia promedio y la reasignación de recursos entre décadas. Los perdedores netos se ubican en el cuadrante inferior izquierdo.
Como regiones ganadoras netas se identifican a Bucaramanga y las principals regiones del país, Bogotá, Medellín, Cali y Barranquilla. El resto parece que durante las últimas dos décadas no logra tener una composición sectorial que potencie el fortalecimiento de la reasignación de recursos hacia sectores con mejor desempeño. El caso más extremo es Cartagena, que se presenta
Cuadro 5.
Descomposición de la eficiencia técnica por décadas
como perdedora neta, ya que pierde eficiencia en promedio y desmejora en el proceso de asignación de recursos. La correlación entre estas dos medidas por regiones es positiva (0,33), lo que parece confirmar un proceso de reforzamiento productivo positivo.
Gráfico 3.
Correlación entre cambios en eficiencia promedio y en reasignación de recursos entre décadas: 1992-2010
Fuente: cálculos propios a partir de la EAM.
Sectorialmente, los ganadores netos son textil y papel. Minerales y otras manufacturas también presentan un buen desempeño, aunque en menor medida. No se observan sectores perdedores netos, solo sectores que únicamente refuerzan el aumento de eficiencia promedio (química, metalurgia, caucho y bienes de capital), o los que solo refuerzan el proceso de reasignación de recursos (alimentación). La correlación entre estas dos medidas también es positiva, aunque muy baja (0,063). Es decir, las condiciones regionales tienen un papel más importante en el desempeño sectorial (en las ganancias de eficiencia y el fortalecimiento de sinergias productivas) que a la inversa. Por tanto, pareciera fundamental centrar la atención en las particularidades regionales al definir la política industrial. El fortalecimiento de los mercados y la competitividad regional condicionan la eficiencia de la industria regional.
Con el fin de identificar cómo la reasignación de recursos ha sido influenciada por procesos de cambios en la especialización sectorial de las regiones, en la concentración de la industria a nivel regional, en la concentración regional de los sectores o en la composición de la actividad a nivel nacional se propone un índice de descomposición dinámica de la eficiencia técnica total (IDDETT). El índice IDDETT constituye un aporte a la literatura, que permite asociar la evolución de la eficiencia técnica al comportamiento de indicadores fundamentales en el análisis de la distribución regional de la actividad económica, lo que lleva a convertir la limitación que supone trabajar con datos agregados (común en muchos países latinoamericanos) en una fortaleza para encuestas exhaustivas como lo es la EAM. Este indicador posibilita cuantificar en qué medida estos factores han potenciado o limitado el crecimiento regional. El índice se define como:
donde ETtT es la media ponderada y 
es la media aritmética de la eficiencia técnica para la industria en el periodo t; y 
es la probabilidad conjunta (PT) del sector j y la región i, en t, es decir, en cuánto participa la región i en el sector j en el empleo industrial en t.
Reemplazando 
en la ecuación (12), el cambio en la eficiencia técnica en el tiempo se puede expresar como:
Según el teorema de Bayes, se puede redefinir la probabilidad total como el producto entre las probabilidades condicional y marginal (pT = pC. pM) y, por tanto, la ecuación (14) se puede reexpresar como:
Descomponiendo la ecuación (14):
donde 
otras dif. 29.
Dado que las probabilidades condicionadas y marginales dependen de si se realiza el análisis por sector o región, se define:
donde P(Rit) = pitM es la probabilidad marginal de la región i en el empleo industrial en t, es decir, representa la participación de la región i en el empleo nacional; y P(Sjt) = pMjt es la probabilidad marginal del sector j en el empleo industrial en t, es decir, representa la participación del sector j en el empleo nacional.
Por tanto, se deduce que para regiones y sectores, respectivamente:
Δpjtc; cambio por diferencias en la especialización sectorial de las regiones
diferencias en la concentración de la actividad nacional por regiones
cambio por diferencias en la concentración sectorial por regiones
: cambio por diferencias en composición sectorial de la industria nacional
El cuadro 6 presenta la descomposición dinámica del componente de asignación de recursos por sector y por región. La variación promedio anual durante el periodo de análisis es bastante baja (-0,00076), con saldo ligeramente positivo durante la década de los noventa y negativo durante el siglo XXI. Sin embargo, oculta una alta heterogeneidad entre regiones y sectores. A nivel de región, existe un efecto positivo tanto de una mayor especialización de las regiones (0,046), como de la mayor concentración de la industria por regiones (0,062). Ambos procesos acentúan la competencia, con lo cual es de esperar que aumente la eficiencia por reasignación. El análisis por sector presenta un importante papel de la concentración de los sectores en determinadas regiones (0,134), mayor aún que los componentes regionales. Sin embargo, el papel de la composición sectorial de la industria es negativo (-0,032). Esto se interpreta como una mayor participación de los sectores menos productivos (aunque este valor se reduce entre las dos décadas). El gráfico 4 muestra que el comportamiento del sector textil está fuertemente influenciado por la concentración de la industria en las regiones. Bogotá es la región más favorecida por la concentración regional de la industria.
La mayor importancia relativa de los factores sectoriales frente a los regionales se explica, entre otros, porque no todas las regiones se benefician en la misma magnitud de este tipo de sinergias. Por el contrario, la concentración sectorial ofrece un beneficio general a pesar del aumento de competencia, en cuanto a que logra reducir de manera considerable los costos de transacción respecto a clientes y proveedores.
En la literatura internacional existe un amplio consenso sobre la importancia de las economías de aglomeración, sobre la competitividad de las regiones (véanse Glaeser et al., 1992; Henderson et al., 1992; Melo et al., 2009; Puga, 2010; Rosenthal y Strange, 2004). La dinámica interna de los mercados tiene un papel fundamental en las posibilidades de las empresas para establecerse, crecer y expandirse hacia otros mercados. Las características propias de las regiones posibilitan la presencia de externalidades del capital humano, tecnológicas
Cuadro 6.
Descomposición de la evolución dinámica de la reasignación productiva para la industria: 1992-2010
a Promedio interperiodo de la suma en t.
Fuente: cálculos propios a partir de la EAM.
y de mercado. En este contexto, pareciera que las regiones con menor desarrollo se vieran atrapadas en sus propias trampas de pobreza por la imposibilidad de generar las dinámicas necesarias.
No obstante, este estudio confirma que en las regiones se conforman nichos específicos de mercado, en función de lo que “mejor saben hacer”. Las regiones son más eficientes en los sectores sobre los cuales tienen una mayor especialización. Por tanto, es posible que esa dinámica interna les pueda generar procesos de diferenciación que les permita posicionarse en el mercado. En este sentido, se confirma la importancia de definir estrategias con base en sectores líderes para impulsar el desarrollo regional en función de sus potencialidades y capacidades, al trazar la política industrial.
Gráfico 4.
Importancia relativa de los componentes de descomposición de reasignación productiva para la industria: 1992-2010
Nota: los valores parciales suman sobre la probabilidad total. Promedio anual 1992-2010.
Fuente: cálculos propios a partir de la EAM.
La situación de Cartagena es un poco desconcertante, sobre todo teniendo en cuenta que posee una de las principales refinerías colombianas y que debido a ello su producto bruto, incluido el petróleo, es bastante alto. Este estudio encontró un decrecimiento continuo en los niveles de competitividad de esta región frente al resto (excluyendo el petróleo) y un decrecimiento en la productividad de uno de los sectores más tradicionales en su composición, como lo es el sector químico. ¿Es posible que la alta especialización de la economía de Cartagena hacia la actividad petrolera haya generado un deterioro en el resto de la actividad industrial regional? ¿Cuál es el punto de inflexión en el que una elevada especialización en determinados sectores puede deteriorar las condiciones económicas y sociales de una región? ¿Cuál es el nivel de eslabonamientos que ha generado esta actividad para el resto de la economía regional (nacional)? Colombia es un caso de estudio bastante interesante en este aspecto, ya que en los últimos años ha realizado grandes esfuerzos en la atracción de capital extranjero y la explotación minera y petrolera. Se reconocen la importancia y trascendencia de estos interrogantes, por lo cual se proponen como líneas de investigación futura.
Se reconoce además la importancia de estimar un modelo de determinantes de la eficiencia, que permita controlar el efecto que tienen otros factores, como el grado de penetración de sectores o regiones en el comercio internacional, las diferencias en dotación de infraestructura, la densidad urbana, la composición tecnológica de los sectores y el grado de interrelación sectorial en cada región, entre otros indicadores de pobreza, desigualdad y educación. No obstante, dada la envergadura metodológica, conceptual y de análisis que implica tal objetivo, se propone su cubrimiento en una nueva publicación.
V. Conclusiones
El objetivo de este estudio es aportar una medida actualizada de la evolución de las diferencias en la productividad time varying por sectores y regiones para la industria colombiana, durante el periodo 1992-2010, e identificar la importancia de los procesos de reasignación de recursos sobre los patrones de competitividad.
Para hacerlo, se emplearon técnicas de fronteras estocásticas de producción time varying, que permiten modelar de manera libre el patrón de evolución temporal para cada unidad de análisis. Los resultados de este estudio confirman importantes diferencias en el patrón de evolución temporal entre regiones y sectores. Se consolida el liderazgo industrial de Medellín, Bogotá y Cali, en contra del rezago de la industria en el resto del país, con un balance bastante negativo para Cartagena. El grupo de sectores que conforman los bienes de capital se consolida como el que tiene mayor eficiencia promedio, situación en la cual se sostiene en el tiempo. La industria textil y la papelera se consolidan como los sectores con mayores ganancias de eficiencia, a pesar de no ser los más eficientes para el conjunto de la muestra. Al valorar la competitividad relativa de las regiones en los sectores, se confirma la existencia de una relación positiva entre la especialización sectorial y la eficiencia técnica.
El análisis de descomposición de varianza de la eficiencia técnica muestra que las diferencias en la evolución entre sectores y regiones puede explicarse tanto por ganancias en la eficiencia promedio, como por la reasignación de recursos al interior de la industria. Estas dos medidas presentan una correlación positiva, que es más fuerte en el análisis regional, lo que parece confirmar la importancia de las características regionales en el reforzamiento productivo de los sectores. En este proceso se identifican como regiones ganadoras netas a Bucaramanga y a las principales regiones del país, Bogotá, Medellín, Cali y Barranquilla. Por el contrario, Cartagena se presenta como perdedora neta.
Sectorialmente, los ganadores netos fueron textil y papel y, en menor medida, minerales y otras manufacturas.
La descomposición dinámica del componente de reasignación de recursos reveló interesantes patrones. La descomposición regional presentó un efecto positivo causado por la profundización en la especialización sectorial de las regiones (0,046) y por la concentración regional de la industria (0,062). El análisis por sector evidenció el importante papel de la concentración de los sectores en determinadas regiones (0,134). Por el contrario, el efecto de reasignación debido a la composición sectorial de la industria fue negativo (-0,032), a pesar de presentar mejoras relativas en la última década. La mayor importancia relativa de la concentración sectorial en determinadas regiones, por una parte, parece confirmar el papel predominante de las características regionales en la evolución de la eficiencia técnica sectorial y, por otra, ratificar la importancia de definir estrategias con base en sectores líderes para impulsar el desarrollo regional (en función de sus potencialidades y capacidades), al trazar la política de desarrollo industrial.
Es valioso impulsar la actividad industrial de las regiones en aquellos sectores en los cuales esta posee ventajas naturales o históricas que sean significativas en el fortalecimiento de sinergias con otros sectores. También es importante fortalecer la red de infraestructuras y apoyar la creación de empresas y su vocación hacia sectores con mayor contenido tecnológico, de modo que esto permita la generación de valor agregado, mejore la competitividad y asegure un posicionamiento en el mercado exterior. Por supuesto, es necesario reconocer que la capacidad de los sectores para generar sinergias productivas no es homogénea y que una excesiva especialización en determinados sectores de actividad podría causar a largo plazo mayores perjuicios que beneficios para la economía en su conjunto.
Reconocimientos
Se agradece la colaboración como asistentes de investigación de Karol Alexandra Cruz, María Isabel Zafra y Beatriz Zúñiga, pertenecientes al Semillero de Investigación en Crecimiento Económico de la Universidad San Buenaventura, Cali. También se agradece a los evaluadores anónimos de la revista por los comentarios y sugerencias a una versión preliminar de este documento, así como a Carlos Humberto Ortiz y José Luis Raymond Bara y a los asistentes al “13th Summer Institute of the Pacific Regional Science Conference Organization - PRSCO 2014” y al “XVI Applied Econsomics Meeting 2013”, organizada por la Asociación Libre de Economía. También se agradece al Departamento de Investigaciones Buenaventuriano de la Universidad san Buenaventura, Cali, por la financiación recibida para la realización de este proyecto.
