Introducción
Con esquemas de inflación objetivo las expectativas de inflación adquieren un papel importante en el seguimiento e implementación de la política monetaria. Más aún, tal y como señalan Huertas, González y Ruiz (2015), es de vital importancia que los bancos centrales anclen las expectativas, de tal manera que se puedan disminuir los costos asociados a la tarea de controlar y reducir la inflación, y así facilitar la conducción de la política monetaria. Debido a lo anterior, gran parte de los modelos teóricos y prácticos desarrollados por académicos y hacedores de política incorporan esta variable (González, Jalil y Romero, 2010). A su vez, los agentes participantes del mercado financiero han incrementado el monitoreo de las expectativas de inflación para tomar sus decisiones de inversión.
Por tanto, es relevante contar con medidas que reflejen de manera adecuada el comportamiento de las expectativas de inflación. En términos generales, las medidas con las que se cuentan son las encuestas de inflación (expectativas directas) o las expectativas que se pueden deducir a partir de los títulos nominales y reales emitidos por los gobiernos (expectativas indirectas). No obstante, dichas medidas presentan ciertas limitaciones. Por una parte, las encuestas se realizan a un conjunto limitado de agentes y para ciertos horizontes de tiempo (por ejemplo, inflación esperada a un año) son menos oportunas, pueden adquirir sesgos asociados a las metodologías de recolección y presentan costos asociados al diseño, recolección, procesamiento y análisis. Por otro lado, las inflaciones implícitas en los bonos reales y nominales (break-even inflation [BEI])5 pueden incluir múltiples elementos como las expectativas de inflación, la prima de riesgo inflacionario, la prima de liquidez, entre otros, lo cual hace más difícil su interpretación directa como medida de expectativas de inflación.
A pesar de sus limitaciones, el BEI es ampliamente utilizado por los agentes y hacedores de política, dada la disponibilidad de información y la posibilidad de calcularlo para un conjunto amplio de períodos de maduración (Melo-Velandia y Granados-Castro, 2010). Es por esto que la descomposición del BEI en sus distintos componentes ha venido cobrando importancia, por lo que han sido desarrollados diferentes métodos para su estimación.
Tal como señalan Abrahams, Adrian, Crump, Moench y Yu (2016), la literatura referente a la estimación de expectativas de inflación a partir de bonos reales y nominales de los gobiernos ha crecido rápidamente. Por ejemplo, Adrian y Wu (2010), Chen, Liu y Cheng (2010), Christensen, López y Rudebusch (2010), García y Werner (2010), Grishchenko y Huang (2013) y Hördahl y Tristani (2010), entre otros. Respecto a documentos de trabajo de diferentes bancos centrales, es posible encontrar literatura en esta línea para el Banco de Japón (Imakubo y Nakajima, 2015), la Reserva Federal (Abrahams et al., 2016), el Banco Central Europeo (Ejsing, García y Werner, 2007), el Bundesbank (Kajutha y Watzkab, 2011), el Banco de Canadá (Christensen, Dion y Reid, 2004), el Banco Central de México (Banco de México, 2013), el Banco Central de Chile (Chumacero y Opazo, 2008) y el Banco de la República (Arias, Hernández y Zea, 2006; Melo-Velandia y Granados-Castro, 2010; Melo-Velandia y Moreno- Gutiérrez, 2011), entre otros.
En términos generales, la literatura señalada descompone el BEI mediante modelos afines gaussianos estimados por máxima verosimilitud, utilizando filtro de Kalman. Generalmente, esta descomposición se realiza en dos factores: expectativas de inflación y prima de riesgo inflacionario. Si bien esta es la norma, varios autores han señalado algunas debilidades de estos modelos. Dentro de las principales desventajas se tiene que la estimación es costosa en términos computacionales, por lo que dichos modelos tienden a utilizar tres componentes o factores latentes para la representación de la estructura a término, no tienen en cuenta la heterogeneidad de la liquidez de los títulos y suponen no correlación sobre los errores de los precios de los rendimientos.
Por tal razón, Abrahams et al. (2016) plantearon un modelo afín para la descomposición del BEI de los bonos del Gobierno de Estados Unidos, que se estima mediante una metodología que utiliza regresiones lineales, basados en Adrian et al. (2013). Dicha metodología permite dejar de lado supuestos mencionados previamente, reduce los costos computacionales, y además permite ajustar por la liquidez de los bonos reales relativa a los nominales. Respecto a este último punto, la literatura ha señalado constantemente la menor liquidez de los bonos atados a la inflación (Dudley, Roush y Ezer, 2009; Sack, 2000) y la necesidad de tener en cuenta la liquidez relativa de los dos tipos de bonos para los análisis referentes al BEI (Pflueger y Viceira, 2013), lo que lleva a que el trabajo de Abrahams et al. (2016) adquiera mayor relevancia en la literatura6.
En Colombia, tal como lo señalan Gómez, Uribe y Vargas (2002), el seguimiento de las expectativas de inflación ha desempeñado un papel importante en el monitoreo de la política monetaria y en la implementación del esquema de inflación objetivo adoptado por el Banco de la República. Trabajos como el de Arango, Flórez y Arosemena (2005), Vargas, González, A., González, E., Romero y Rojas (2010) y Huertas et al. (2015), entre otros, utilizan medidas de expectativas de inflación para el análisis de política monetaria, el desarrollo de modelos macroeconómicos y la evaluación de pronósticos de inflación. Lo anterior señala la importancia de contar con mejores indicadores de expectativas de esta variable.
Por su parte, son varias las encuestas de inflación con las que se cuenta desde que se adoptó el esquema monetario actual. La mayoría de estas encuestas presentan una periodicidad mensual y consideran en general las expectativas para el siguiente mes, fin de año y doce meses adelante7. De esta manera, no se cuenta con encuestas que permitan tener una medida de expectativas de inflación para plazos superiores a los previamente señalados8. Ante esto, el BEI se ha convertido en una medida de expectativas de inflación ampliamente utilizada dentro del análisis de la política monetaria y en las decisiones de los inversionistas en Colombia.
A pesar de esta creciente relevancia, en Colombia la literatura respecto a la descomposición del BEI no es muy extensa. En el límite de nuestro conocimiento, Arias et al. (2006), Melo-Velandia y Granados-Castro (2010), Melo-Velandia y Moreno-Gutiérrez (2011) y Ríos y Girón (2013), han realizado trabajos asociados a la descomposición o corrección del BEI de los bonos del Gobierno colombiano. Específicamente, Arias et al. (2006) utilizan un modelo de valoración con el fin de estimar una medida de compensación de inflación, mientras que Melo-Velandia y Granados-Castro (2010), Melo-Velandia y Moreno-Gutiérrez (2011) y Ríos y Girón (2013) estiman modelos afines, con ciertas diferencias, para descomponer el BEI en prima de riesgo inflacionario y expectativas de inflación. Un punto en común que tienen los documentos es el hecho de señalar el problema en la descomposición o estimación referente a la menor liquidez relativa de los títulos denominados en Unidad de Valor Real (UVR), el cual, si bien los autores lo señalan, ninguno incorpora alguna medida para corregirlo.
Frente a este último punto, como se puede observar en el apéndice A, los bonos de deuda pública del Gobierno colombiano denominados en UVR, en general, son significativamente menos líquidos que los bonos denominados en pesos. Además, debido al esquema de colocación que históricamente se ha realizado para los títulos UVR, desde el 2004 se puede encontrar que por momentos y para ciertos vencimientos (por ejemplo, 1, 2 y 10 años) no hay títulos disponibles en el mercado.
Por tanto, con el fin de mejorar las medidas relacionadas con expectativas de inflación, particularmente aquellas asociadas al BEI de los bonos del Gobierno colombiano, el presente documento estima y descompone el BEI en expectativas de inflación, prima de riesgo y prima de liquidez, utilizando la metodología desarrollada por Abrahams et al. (2016). Como se mencionó, dicha metodología es menos costosa en términos computacionales y tiene en cuenta la prima de liquidez de los bonos, lo cual no ha sido contemplado previamente para el caso colombiano. Al considerar esta prima, se debería obtener una mejor estimación de las expectativas de inflación basadas en el BEI.
El documento se divide en tres secciones después de esta introducción. La primera sección describe la metodología empleada para la descomposición del BEI, mientras que en la segunda sección se presentan los resultados. Por último, se realizan algunos comentarios finales.
I. Metodología
En esta sección se presenta el modelo econométrico utilizado, el método de estimación y la construcción de la estructura a términos de los bonos nominales e indexados por inflación siguiendo la metodología de Abrahams et al. (2016), de ahora en adelante denominada AACM.
A. Variables de estado y factor de descuento estocástico
Siguiendo a AACM, el vector de variables de estado Xt, que en la práctica corresponden a componentes principales de los rendimientos nominales o reales, variables macroeconómicas o indicadores de liquidez, entre otros, de dimensión K × 1 puede ser modelado por el siguiente proceso VAR(1):
Donde las innovaciones υt+1 |X t siguen una distribución normal, N(0, Ʃ). Se asume que para los precios de un bono con vencimiento n en el período t, t, 
, existe un factor de descuento estocástico exponencialmente afín que valora estos activos con la siguiente ecuación:
Además, se define rt como la tasa libre de riesgo; y, según Duffee (2002), se asume que los precios de riesgo del mercado siguen la forma:
El término λt es de gran importancia estadística y económica, ya que caracteriza el riesgo asociado a cada variable de estado. Este se puede desagregar en una constante (λ0), relacionada con el nivel de estos precios, y en un vector (λ1) asociado a la relación entre el precio y estas variables.
Por último, se definen los parámetros que caracterizan la dinámica de los activos con la medida de valoración (ℚ), la cual permite caracterizar el comportamiento del mercado en ausencia de arbitraje, pero con presencia de riesgo (λ1, λ0 ≠ 0):
Estos son importantes para calcular las recursiones utilizadas para desagregar los bonos nominales, indexados por inflación y BEI en 3 componentes: medidas de riesgo neutral, primas de riesgo y primas de liquidez. Estas son presentadas en las siguientes secciones.
B. Bonos nominales
En los modelos afines, el logaritmo de los precios para un bono descontado por una tasa libre de riesgo con vencimiento n en el período t, es lineal en las variables de estado siguiendo la forma:
Lo anterior implica que la tasa libre de riesgo es afín en las variables de estado:
Imponiendo condiciones de no arbitraje, es posible reescribir esta relación de forma iterativa a través del siguiente sistema de ecuaciones:
lo cual permite tomar como valores iniciales B1 = δ1 y A1 = δ0.
Por último, se denota el exceso de retorno (en logaritmos) para un bono como 
, definido de la siguiente manera:
Reemplazando (6) y (7) en (11), e imponiendo las ecuaciones recurrentes se obtiene la siguiente expresión:
donde 
. Es de notar que esta representación facilita el procedimiento de estimación de los parámetros que caracterizan los excesos de retorno nominales presentados en la sección I.F.1.
C. Bonos indexados por inflación (reales)
A continuación, se extiende el marco teórico de manera que puedan tenerse en cuenta activos indexados por inflación. Siguiendo a AACM, sea Qt un índice de precios en el tiempo t, y sea 
el precio en el período t de un activo indexado por inflación con valor facial 1, el cual paga la cantidad 
en el período t + n; entonces, el precio de este activo satisface la siguiente ecuación de valoración:
Donde 
el valor esperado con la medida de valoración. Sea 
la inflación obtenida para un período. Por tanto, se cumple lo siguiente:
Además, se asume de forma similar al caso de los nominales que el logaritmo de estos precios es afín en las variables de estado:
Esto implica a su vez que la inflación para un período es una función lineal de las variables de estado:
donde π0 es un escalar y π1 es un vector de tamaño K × 1. Es de notar que la ecuación (13) puede reescribirse en términos de un bono indexado que se compra un período más adelante:
Esta representación permite derivar un sistema de ecuaciones iterativo para la ecuación (15) similar al de los bonos nominales, el cual tiene la siguiente forma:
donde el parámetro asociado a la tasa de corto plazo real se define como δ0,R = δ0 − π0. Por otra parte, es de notar que el sistema planeado permite tomar como valores iniciales B1,R = δ′1 y A1,R = δ0,R. Lo anterior implica que los excesos de retorno para estos activos vienen dados por:
Sumando la inflación para un período en ambos lados de la ecuación (21), y combinando esta expresión con las ecuaciones (16), (18) y (19), se obtiene la siguiente expresión:
donde 
Finalmente, se agrupan los excesos de retorno nominales de la ecuación (12) junto con los indexados por inflación de la ecuación (22) en el vector R9, obteniendo el siguiente sistema de ecuaciones de forma compacta:
donte 
, 
y NN, NR corresponden al número total de vencimientos para los activos nominales e indexados por inflación, respectivamente.
D. Expectativas de inflación
Dado el modelo afín presentado en las secciones I.B y I.C es posible estimar el BEI y las expectativas de inflación con la medida de valoración y de riesgo neutral para cualquier horizonte de tiempo. En este contexto, el BEI 
se calcula como la diferencia entre los rendimientos nominales 
e indexados por inflación 
para un horizonte de tiempo n, cuya expresión es la siguiente:
Con la medida de riesgo neutral, se cumple que Λ = [λ0 λ1] = 0 y por tanto, los rendimientos nominales e indexados por inflación de riesgo neutral, así como las expectativas de inflación, se obtienen reemplazando los parámetros μ̃ y ϕ̃ por sus versiones ajustadas por riesgo (IK − ϕ) µX y ϕ en las ecuaciones (8), (9), (18) y (19). La expresión que rige estas expectativas de riesgo neutral es la siguiente:
Por tanto, la prima de riesgo inflacionario en el período t para el horizonte de tiempo n, definida como la compensación que reciben los inversionistas por asumir un riesgo inflacionario, puede calcularse como la diferencia entre el BEI y las expectativas de inflación, lo cual es equivalente a restar la prima por término de los activos nominales de la prima por término de los activos indexados por inflación, es decir:
Agrupando por tipo de activo, se obtiene la siguiente expresión:
donde 
denotan la prima por término de los activos nominales e indexados por inflación para el período t con vencimiento n, respectivamente.
Hasta el momento fue presentada la descomposición del BEI en sus dos elementos tradicionales: expectativas y prima de riesgo inflacionario. Este marco teórico se amplía en la siguiente sección, realizando la inclusión de factores de liquidez, los cuales permiten realizar la descomposición incluyendo una prima de liquidez asociada a estos activos.
E. Efectos de liquidez
La manera de modelar efectos de liquidez para los bonos en este marco teórico se presenta a continuación.
Sea Lt una variable de estado que captura la liquidez de los activos, la cual se asume como observada; entonces, al expandir el conjunto de variables de estado 
, se mantienen las relaciones establecidas en las ecuaciones (8), (9), (18) y (19). Esta expansión permite obtener la prima de liquidez para estos activos, así como las medidas ajustadas por liquidez en todos los casos. Lo anterior se logra restringiendo a O la ponderación asociada al factor de liquidez en cada caso 
10.
Luego es posible calcular los componentes de liquidez en el período t con vencimiento n con cada medida como 
para los bonos nominales, 
para los bonos indexados por inflación. Por tanto, la prima de liquidez nominal y real puede calcularse como se muestra a continuación:
Por otro lado, el componente del BEI asociado a la prima de liquidez puede obtenerse de forma similar a la prima de riesgo inflacionario, restando las respectivas primas de liquidez de bonos nominales e indexados por inflación, es decir:
Los resultados de estas descomposiciones se presentan en la sección II.C.
F. Estimación
En esta sección se muestra el procedimiento utilizado para estimar los parámetros del modelo que describe los excesos de retorno dados en la ecuación (23). Posteriormente, se discute la estimación de los parámetros (δ, δ′1) y (π0, π1) que caracterizan la tasa libre de riesgo y la inflación.
1. Estimación de los parámetros
La metodología utilizada para estimar los parámetros del modelo corresponde al siguiente procedimiento propuesto por AACM, el cual es similar al estimador en tres etapas de Adrian et al. (2013) y es presentado a continuación.
Primero, a partir de la ecuación (23) se agrupan los datos de la siguiente manera:
donde R es de orden N × T, X_y X son matrices de tamaño K × T de los datos agrupados de Xt–1 y Xt, respectivamente, y ιT es un vector de orden T × 1 de unos. La matriz E corresponde a los errores de medición de los retornos agrupados, donde la n-ésima columna, en, satisface 
. Dada esta representación, se realiza el siguiente procedimiento:
0. Se extraen los primeros KN componentes principales sobre los rendimientos de la curva cero cupón nominal a través del método de descomposición en valores singulares11. Una vez obtenidos, estos factores son estandarizados. Después, se obtienen los primeros KR componentes principales utilizando la misma metodología sobre los residuales de regresiones para rendimientos de la curva cero cupón de bonos indexados por inflación sobre los componentes principales nominales y el factor de liquidez. Estos KN +KR +1 variables corresponden al vector de variables
utilizados en la estimación.1. Posteriormente, se estima la regresión descrita en (1) usando mínimos cuadrados ordinarios (MCO) para las variables centradas en media, utilizando los promedios muestrales obtenidos anteriormente como estimadores de µX. Además, de esta estimación se obtienen los residuals, υ̂t+1, y su matriz de varianza-covarianza, definida como
, donde V̂ de dimensión K × T se obtiene agrupando las innovaciones estimadas. Es de notar que Stock y Watson (2002) (en adelante SW) muestran que los estimadores de modelos lineales provenientes de estos componentes son consistentes cuando el tamaño de la muestra y el número de series tiende a infinito con el supuesto de estacionariedad en el sistema. La estimación de esta primera etapa es similar a la del modelo dinámico presentado por SW en su segunda etapa, ya que los factores nominales y reales son variables latentes obtenidas mediante el método de análisis de componentes principales, los cuales se utilizan para estimar un modelo VAR.-
2. Se estima la ecuación (30) a través de una regresión SUR, obteniendo los estimadores
. Utilizando los residuales estimados de esta regresión Êols, se obtiene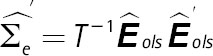 
. Entonces, el estimador de ϕ̃ es:
Después, se estima la regresión SUR:
, de la cual se obtienen estimadores más eficientes de α y B, los cuales se denominan como α̂gls y B̂gls. Por último, se estima μ̃ a través de la siguiente expresión:
donde γ̂gls definida en la sección I.C se construye utilizando B̂gls y Ʃ̂.
-
3. Dadas las relaciones descritas en las ecuaciones (4) y los estimadores μ̂x y ϕ̂, los precios del riesgo del mercado se obtienen a través de las siguientes expresiones:
AACM muestran que los errores estándar asintóticos de los estimadores (31) y (32) se pueden obtener del siguiente resultado:
Las expresiones para
se presentan en el apéndice C.
2. Descomposición del BEI y estimación de los parámetros asociados a la tasa libre de riesgo y la inflación
Antes de calcular el proceso iterativo para los bonos nominales, es necesario estimar (δ0, δ′1) asociados a la tasa libre de riesgo. Dado que esta tasa es observada y afín en las variables de estado, estos parámetros se obtienen al estimar una regresión de los rendimientos nominales correspondientes al primer mes (n = 1) en unidades porcentuales, contra una constante y los factores obtenidos Xt, es decir: 
, donde 
denota el error de valoración del rendimiento nominal con vencimiento a un mes.
Por otra parte, para resolver las recursiones presentadas en (18) y (19), es necesario conocer los parámetros π0 y π1 que caracterizan la evolución de la inflación en términos de las variables de estado. En el apéndice D se muestra que π0 representa la inflación de largo plazo del modelo, así como el procedimiento realizado para estimar π0 y π1.
Una vez se tienen estimados estos parámetros, se realiza el proceso recurrente para los bonos nominales descrito en (36) y (37), y de forma similar para los bonos reales; en esta etapa se obtienen los rendimientos estimados nominales y reales, ajustados por liquidez, 
. Este procedimiento se repite suponiendo que los precios del riesgo son cero (Λ = 0); de esta forma, se obtienen los rendimientos estimados con la medida de riesgo neutral, 
.12
Las medidas anteriores permiten calcular las primas por término 
y de riesgo inflacionario 
de acuerdo con la ecuación (26). Como paso siguiente se calcula el BEI estimado por el modelo 
y las expectativas de inflación 
siguiendo las ecuaciones (24) y (25)13. De forma seguida, la estimación de la prima de liquidez de los bonos nominales 
y reales 
se realiza a partir de las ecuaciones (27) y (28); por último, el componente del BEI asociado a la liquidez 
se estima a partir de la ecuación (29), de forma que 
.14
II. Resultados
Esta sección se divide de la siguiente manera: descripción de los datos utilizados, resultados de las estimaciones del modelo y análisis de bondad de ajuste para el mismo; por último, se presentan las descomposiciones de los rendimientos nominales y reales obtenidas en el proceso recurrente estimado en las ecuaciones (8), (9), (18) y (19). Estas incluyen la descomposición del BEI en expectativas de inflación, prima de riesgo inflacionario y componente de liquidez.
A. Descripción de los datos utilizados
Los rendimientos, 
, asociados a la curva cero cupón nominal y real, respectivamente, son calculados a partir de los parámetros de la metodología propuesta por Nelson y Siegel (1987) para los títulos de tesorería (TES) en pesos y en UVR transados en el Sistema Electrónico de Negociación (SEN) y Mercado Electrónico de Colombia (MEC), con vencimientos (n) entre 1 y 96 meses15. Como tasa libre de riesgo se utiliza la tasa interbancaria (TIB) obtenida en la página web del Banco de la República, y como medida Qt se toma el índice de precios al consumidor (IPC) en frecuencia mensual, el cual se encuentra disponible en la página web del Departamento Administrativo Nacional de Estadística (DANE). La muestra utilizada incluye los períodos de frecuencia mensual comprendidos entre junio del 2004 y abril del 2015.
Por otra parte, siguiendo la metodología de AACM, el factor de liquidez Lt se construye de la siguiente manera: primero, se obtienen los residuales de la estimación de la curva de rendimiento cero cupón para los TES en UVR por la metodología de Diebold y Li (2006)16. Autores como Fleming (2000) y Hu, Pan y Wang (2013) utilizan este tipo de residuales como una medida de liquidez, puesto que “grandes desajustes en los rendimientos pueden implicar estrés en el mercado o la inhabilidad de los inversionistas para aprovechar errores de valoración percibidos por el mercado” (AACM). Segundo, se toma el promedio móvil de 13 semanas17 de la razón de montos transados de TES en pesos respecto a UVR, el cual captura la liquidez de los títulos nominales relativa a los reales. Posteriormente, estas series son estandarizadas y se calcula Lt en frecuencia diaria como el promedio simple entre estas dos medidas. Por último, con el objetivo de garantizar que esta medida sea positiva, a este promedio se le suma el mínimo de esta serie diaria y se lleva a frecuencia mensual tomando el último dato de cada mes.
Teniendo en cuenta a Scheinkman y Litterman (1991), se calculan los primeros KN = 3 componentes principales sobre los rendimientos de los TES en pesos con vencimientos n = 3, 4, 5,…, 96 meses. Con el objetivo de reducir la posible multicolinealidad entre los componentes principales de las curvas nominales y reales, se obtienen los KR = 2 primeros componentes principales de los residuales obtenidos a partir de regresiones de los rendimientos de los TES en UVR sobre los 3 componentes nominales y el factor de liquidez, con vencimientos n = 24, 25, 26…, 96 meses18. En este procedimiento se encuentra que aproximadamente el 99,73% de la variabilidad de estos residuales se explica por estos 2 factores.
Por tanto, el modelo estimado incluye KN = 3 factores nominales, KN = 2 factores reales, y 1 factor de liquidez, los cuales corresponden al conjunto de KN + KR + 1 = 6 variables estado 
utilizadas para estimar la ecuación (1). Posteriormente, se calculan los precios asociados a estos rendimientos y los excesos de retorno, a partir de la ecuación (11) para los vencimientos n = 6, 12, 24, 36, 48, 60, 72, 84 y 96 meses para los títulos nominales, mientras que para los reales se utiliza la ecuación (21) para los vencimientos n = 24, 36, 48, 60, 72, 84, y 96 meses; de esta manera, el número de vencimientos para realizar la estimación previamente descrita es NN = 9 y NR = 7, lo cual da un total de N = 16.
B. Estimación del modelo de 6 factores y bondad de ajuste
En esta sección se presentan las estimaciones de los parámetros asociados a los precios de riesgo del mercado (λ0 y λ0) del modelo, a partir de los 6 factores previamente descritos y del procedimiento de estimación en 3 etapas mostrado en la sección I.F.1. Además, se presentan las medidas de bondad de ajuste calculadas para el proceso recurrente descrito en las secciones I.B y I.C.
En primer lugar, se presentan las medidas diagnósticas utilizadas para comprobar una adecuada especificación y ajuste del modelo estimado para realizar las respectivas descomposiciones del BEI y de las tasas de interés nominales y reales. Una manera de verificar una apropiada bondad de ajuste entre los rendimientos y su aproximación afín descrita en las ecuaciones (6) y (15), así como verificar una adecuada estimación de las descomposiciones descritas en la sección I.D, consiste en realizar un análisis descriptivo sobre los residuales obtenidos por las recursiones, el cálculo del BEI y las regresiones de los excesos de retorno. En el apéndice E se presentan estas estadísticas19.
Por otra parte, en la figura 5 se presenta el rendimiento promedio para cada vencimiento de los bonos nominales y reales observados y estimados, estos muestran el ajuste promedio de la curva de rendimiento en ambos casos a lo largo de la estructura a término20. Al igual que los resultados de las tablas anteriormente descritas, se observa que no existen indicios de un mal ajuste del modelo; no obstante, en los últimos vencimientos se observa una leve tendencia a desmejorar el ajuste en los rendimientos reales.
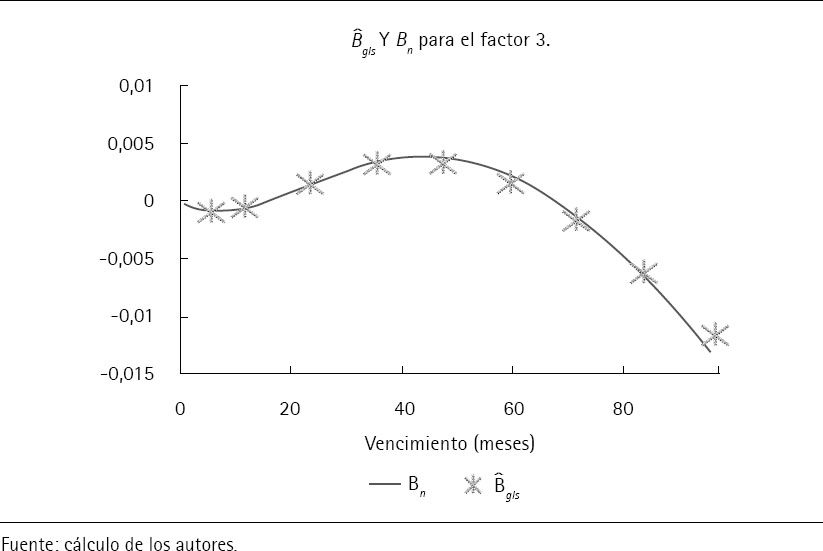
Para verificar si el proceso iterativo utilizado para descomponer estas tasas es adecuado, en el apéndice G se muestran las figuras comparativas entre Bgls, N = (B1,…,BNN) y B para los bonos nominales, donde B se obtiene a través de las recursiones presentadas en las ecuaciones (8) y (9). En el caso de los bonos indexados por inflación, esta comparación se realiza entre Bgls, R = (B1,R + π1,…, BNN+ π1) y BR + π1 obtenido en las recursiones (18) y (19). Además, es de notar que Bgls, N y Bgls, R se estiman en la segunda etapa del procedimiento de estimación presentado en la sección I.F.1. Los resultados de estas figuras muestran que estos términos son similares para ambos activos.
Por último, al realizar el procedimiento de estimación descrito en el apéndice D se encuentra una inflación de largo plazo, π̂0, de 3,2% anual, con un error estándar de 0,301, la cual se encuentra dentro del rango meta del Banco de la República (2% - 4%) y es cercana a la meta puntual del 3%.
Dados los resultados de estas medidas, es posible concluir que el proceso iterativo utilizado es una aproximación adecuada de la estructura a plazo de las tasas de intereses nominales, reales y el BEI. Por tanto, se presentan a continuación los resultados de la estimación de los coeficientes asociados a los precios del riesgo del mercado (λ0 y λ1), así como algunas pruebas de hipótesis que permiten evaluar la adecuada especificación del modelo.
La evaluación de la significancia conjunta e individual de los parámetros asociados a los precios de riesgo de mercado se realiza mediante un test de Wald propuesto por AACM21 utilizando los errores estándar obtenidos en el apéndice C.
Los valores p de las pruebas de significancia conjunta se reportan en las dos últimas columnas del cuadro 1. Estos resultados muestran que los precios de riesgo del mercado son significativos para el nivel, pendiente y curvatura de la curva cero cupón nominal y ambos factores provenientes de los rendimientos de los TES en UVR, lo cual implica que ambas estructuras a término responden significativamente de forma conjunta ante cambios en el precio del riesgo asociado a estos factores. En línea con lo anterior, se espera que cambios en el nivel, pendiente y curvatura de la curva cero cupón nominal impliquen movimientos sobre las estructuras a término nominales y reales, tal como es sugerido por AACM; por tanto, es de esperar que la dinámica de los precios de los activos con la medida de valoración en el proceso iterativo depende en gran medida de los factores asociados a ambas curvas.
Cuadro 1.
Estimación de los parámetros Λ para el modelo de 6 factores
[i] Nota. Λ= [λ0, λ1] = [λ0, λ1,1, λ1,2, λ1,4, λ1,5, λ1,6]. Los valores P se encuentran entre paréntesis y corresponden a los de una prueba t para cada coeficiente. En negrita se presentan los coeficientes significativos al 10%, X1, X2 y X3 representan el nivel, pendiente y curvatura de la curva de rendimiento cero cupón nominal, respectivamente; X4 y X5, representan los 2 primeros componentes principales obtenidos de los residuales de los rendimientos de los TES en UVR sobre X1, X2, X3 y factor de liquidez, respectivamente. Por último, X6 representa el factor de liquidez.
Cuadro 2.
Estadísticas descriptivas de 
para los TES en pesos
Cuadro 3.
Estadísticas descriptivas de 
para los TES en UVR
Cuadro 4.
Estadísticas descriptivas de 
para el BEI
De forma similar, para el caso nominal Espinosa-Torres et al. (2014) encuentran que la estructura a termino de los TES en pesos responde de forma significativa ante movimientos en los precios del riesgo asociados a los factores de la estructura a termino nominal, resultado que por lo general se encuentra en la literatura (Adrian et al., 2013; Cochrane y Piazzesi, 2005; Cochrane y Piazzesi, 2008; Scheinkman y Litterman, 1991).
Además, en el cuadro 1 se evalúa la significancia individual para determinar la manera como cada uno de los factores afectan a los precios del riesgo. Para el precio del riesgo asociado al primer factor (X1) se encuentra que los coeficientes del factor 1, 5 y 6 (λ1,1, λ1,5, y λ1,6) son significativos, lo cual indica que los factores relacionados con el nivel de la curva cero cupón nominal, el primer factor real y la liquidez afectan al precio del riesgo asociado a X1.
En el caso de los parámetros del segundo factor (X2), este se ve afectado únicamente por movimientos en los precios del riesgo reales y el factor de liquidez, esto sugiere que los rendimientos de los TES en pesos se ven afectados ante cambios en el mercado de UVR. Para la curvatura de los bonos nominales (X3) se encuentra que tanto el coeficiente asociado a su propio factor (λ1,3) como el del segundo componente de los rendimientos reales y el factor de liquidez son significativos, lo cual sugiere que el mercado de TES nominales puede no ser demasiado profundo, siendo susceptible a movimientos en otros mercados y a una compensación por liquidez propia de estos. Finalmente, se observa que de forma individual los precios del riesgo asociados a los factores reales solo responden ante cambios en sus propios factores y su liquidez. En particular, es de notar que, debido a que estos factores son ortogonalizados a partir de los bonos nominales, el segundo factor no depende de la liquidez, lo que implica que para este caso particular los precios del riesgo asociados a este factor solo responden a los movimientos del mercado de TES en UVR.
Posteriormente, se estiman las recursiones descritas en las ecuaciones (8), (9), (18) y (19) con el objetivo de desagregar las tasas de rendimiento nominal, real y BEI en sus tres componentes: tasas de riesgo neutral, prima por término o de riesgo y prima de liquidez, los cuales son presentados y analizados en la siguiente sección.
C. Descomposiciones de las tasas
En la figura 1 se presenta la descomposición de los rendimientos nominales y reales: prima por vencimiento, rendimiento de riesgo neutral y componente de liquidez22.
Figure 1.
Descomposiciones de los TES en pesos y UVR para vencimientos a 2 (superior), 5 (medio) y 8 (inferior) años
Figure 1a.
Descomposiciones de los TES en pesos y UVR para vencimientos a 2 (superior), 5 (medio) y 8 (inferior) años
Figure 1b.
Descomposiciones de los TES en pesos y UVR para vencimientos a 2 (superior), 5 (medio) y 8 (inferior) años
En general, los resultados son los esperados. En línea con los hallazgos de Espinosa-Torres, Melo-Velandía y Moreno-Gutiérrez et al. (2014), en la descomposición de los bonos nominales y reales se pueden observar tres hechos relevantes: en primer lugar, se observa que a medida que aumenta el plazo, la prima por término es mayor y más volátil. En segundo lugar, se encuentra que a medida que el plazo es menor, el rendimiento de riesgo neutral explica la mayor parte del movimiento de las tasas de interés de los títulos nominales y reales, lo cual puede asociarse a la transmisión de política monetaria (Becerra y Melo, 2009; Cochrane y Piazzesi, 2008). En tercer lugar, se observa que la prima por vencimiento es decreciente para los dos tipos de títulos, esto puede ser explicado por la mayor profundización del mercado de títulos del Gobierno, las mejores condiciones macroeconómicas, el otorgamiento del grado de inversión por parte de las calificadoras de riesgo y las amplias condiciones de liquidez a escala internacional.
Además, se puede observar que las primas por vencimiento y, en algunos casos, los componentes de liquidez incorporan eventos de estrés financiero. El caso más evidente es aquel evento en el que se registró una fuerte sustitución de títulos de deuda del Gobierno por cartera por parte de bancos locales entre febrero y julio del 2006, momento en el cual se observan movimientos importantes tanto en la prima por vencimiento como del componente de liquidez. Otros eventos relevantes que particularmente se observan en la prima por vencimiento (Espinosa-Torres et al., 2014), son la crisis financiera internacional (septiembre-octubre del 2008) y su transmisión a economías emergentes (enero-agosto del 2009), y el anuncio por parte de la Fed de un posible inicio del tapering (mayo-julio del 2013).
En la figura 2 se puede observar la descomposición del BEI en expectativas de inflación, prima de riesgo inflacionario y componente de liquidez. En cuanto a las expectativas de inflación, se observa que a medida que aumenta el plazo esta es menos volátil y en términos generales ha venido disminuyendo en el tiempo, lo que hace evidente la existencia de credibilidad en el Banco de la República y su meta de inflación. En línea con esto, se aprecia que, posterior a la crisis, las expectativas se han mantenido dentro del rango meta del Banco de la República para los diferentes plazos. Este hecho también es soportado por el valor estimado, mediante el modelo de la inflación de largo plazo (3,2%).
Figure 2.
Descomposiciones del break-even inflation (BEI) para vencimientos a 2 (izquierda), 5 (derecha) y 8 (inferior) años
Por otra parte, los resultados obtenidos indican que a medida que aumenta el plazo la prima de riesgo inflacionario es mayor, lo cual es acorde con la literatura pertinente, ya que presenta evidencia asociada frecuentemente a la hipótesis de expectativas (Gürkaynak, Sack y Wright, 2010; Haubrich, Pennacchi y Ritchken, 2012; Hördahl y Tristani, 2012).
De acuerdo con lo anterior se puede observar que la prima de riesgo inflacionario para 2 años es baja, lo que permite inferir que el BEI para este plazo es una medida relativamente apropiada de las expectativas de inflación. Además, se encuentra que para plazos superiores, la prima de riesgo inflacionario ha disminuido en el tiempo, lo que en parte puede obedecer al aumento de la confianza en la política monetaria por parte de los agentes, particularmente luego de que en octubre del 2009 se estableciera la meta de inflación en 3%. Como resultado específico, se puede apreciar que a partir de junio del 2011 esta prima ha sido negativa y actualmente es cercana a 0 para vencimientos a 5 y 8 años. Este último punto puede obedecer a un mayor apetito y menor riesgo asociado a los TES en pesos debido a la importante caída de la prima por vencimiento de estos títulos ante las mejores condiciones de mercado mencionadas y que recaen principalmente sobre estos (por ejemplo, la mayor entrada de extranjeros se registró en el mercado de TES en pesos).
Por último, dentro de los resultados se encontró que el componente de liquidez es muy pequeño en la mayoría de los períodos analizados. Sin embargo, es posible observar que dicho componente toma valores mayores para ciertos eventos como el asociado a la sustitución de los títulos del mercado de deuda pública en el 2006 por parte de los bancos, evento que generó fuertes presiones de liquidez sobre el mercado, particularmente el de UVR.
III. Comentarios finales
En el presente documento se estima y descompone el BEI asociado a los bonos del Gobierno colombiano. Lo anterior se realiza mediante la metodología propuesta por AACM, la cual permite controlar por un componente de liquidez relativo entre los bonos nominales y reales.
En términos generales, se puede observar que los resultados para Colombia son acordes a lo esperado. Para el caso de las tasas nominales se encuentran rendimientos de riesgo neutral y prima por término similares a las halladas por Espinosa-Torres et al. (2014). En general, se encuentra que la aproximación afín valora de forma precisa ambos tipos de rendimientos, lo cual sugiere que la descomposición del BEI es adecuada. Los resultados de esta descomposición muestran evidencia para concluir que los agentes del mercado han incrementado la credibilidad en el Banco de la República y su meta de inflación con el paso de los años.
Por otro lado, los resultados sugieren que el BEI es una medida relativamente apropiada de las expectativas de inflación en el corto plazo (2 años). Además, estos sugieren que los efectos de liquidez son cercanos a 0 para casi todo el período muestral analizado (independiente del vencimiento), salvo por algunos eventos como el del primer semestre del 2006, en el cual se observa una prima de liquidez mayor.
Finalmente, es de notar que la estimación y descomposición del BEI puede ser un insumo importante para el seguimiento y análisis de las expectativas de inflación por parte del banco central y los analistas financieros. Por tal motivo, cobra relevancia desarrollar estudios futuros referentes a la transmisión de la política monetaria, la relación de los componentes del BEI con variables macroeconómicas y el pronóstico de la inflación.
Agradecimientos
Agradecemos al Banco de la República por proporcionar los datos necesarios para realizar el estudio y a los dos árbitros por sus comentarios, los cuales fueron de gran ayuda para mejorar el contenido del artículo.
Apéndice A. Liquidez relativa de los bonos del Gobierno colombiano denominados en pesos y en UVR
En la figura 3, es posible observar varios indicadores que permiten obtener una noción de la liquidez de los TES UVR relativa a la de los TES en pesos.
En primer lugar, las barras negras muestran el monto promedio mensual de negociaciones de TES UVR respecto al de los TES en pesos. Entre junio del 2004 y junio del 2015, en promedio los montos negociados de UVR han representado el 3,7% de los montos negociados de TES en pesos23, lo cual muestra que en términos relativos los montos de negociación en el mercado de UVR son bajos y no son representativos respecto al total del mercado de bonos del Gobierno colombiano.
En segundo lugar, las líneas punteadas (UVR) y de rayas (pesos) representan el número de títulos que en promedio se negociaron diariamente durante cada mes. Como se puede observar la cantidad de títulos negociados de TES en pesos es considerablemente mayor a la de los títulos denominados en UVR. En promedio el número de bonos UVR negociados a lo largo de la muestra fue de 4,3 títulos, mientras que el de pesos se ubica en 11,8324.
Finalmente, el área gris representa los plazos de los TES UVR con los que en promedio cuenta el mercado por mes. Como se puede observar durante períodos considerables de tiempo, no se ha contado con plazos superiores a 8 años (incluso 6 años) ni con plazos inferiores a uno (incluso 2 años). Lo anterior refleja la falta de oferta de títulos para ciertos vencimientos.
Apéndice B. Ecuaciones con la existencia de efectos de liquidez
A continuación se presentan las ecuaciones del modelo para los bonos nominales incluyendo el factor de liquidez Lt. Es de notar que el procedimiento es el mismo para los bonos indexados por inflación.
La relación afín del sistema expandido para los bonos nominales viene dada por la siguiente expresión:
Reescribiendo esta relación de forma compacta, se obtiene:
donde 
.
Imponiendo condiciones de no arbitraje, es posible reescribir esta relación de forma iterativa a través del sistema de ecuaciones (8) y (9) expandido por liquidez:
En particular, el rendimiento nominal 
estimado puede escribirse de la siguiente forma:
Por tanto, para descomponer este rendimiento estimado se imponen las restricciones 
, lo cual permite calcular el rendimiento nominal estimado 
y de riesgo neutral 
ajustados por liquidez. Entonces, la prima por término ajustada por liquidez se calcula como la diferencia entre estas dos variables.
Por último, la prima de liquidez, 
se calcula como se indicó en la sección I.E. Entonces, el rendimiento nominal observado se compone de la siguiente manera:
donde 
, denota la prima por término nominal ajustada por liquidez.
En el caso de los bonos indexados por inflación el procedimiento abordado es similar, de forma que las medidas del BEI se obtienen de igual manera a lo explicado en la sección I.D teniendo en cuenta esta modificación.
Apéndice C. Derivación de las matrices de varianza covarianza
En este apéndice se resume la derivación realizada por AACM para las matrices de varianza-covarianza 
, especificadas en la ecuación (35).
Sean 
los estimadores de una regresión MCO particionada de la ecuación (30). Además, definiendo 
, y realizando la partición de la matriz de varianza covarianza con la siguiente expresión:
Los autores demuestran que 
donde
Dado que Xt sigue un proceso VAR, con los supuestos convencionales se cumple que:
donde
lo cual implica que 
.
Mediante un procedimiento similar se encuentra la matriz de varianza para λ0. Se define 
como la matriz de conmutación de orden mn × mn tal que para una matriz Am×n se cumple que 
como la matriz particionada diagonal NK × N con Bi como la iésima entrada de la diagonal, CB = (vec(B1B1'),…,vec(BNBN')), ρ1, como un vector (K + 1) × 1 cuyo primer elemento es igual a 1 y el resto son iguales a 0, y las siguientes expresiones:
donde Mι = IT − χ'(χχ')−1 χ; entonces, se cumple que
con:
donde:
Entonces, 
con 
. Por último, la covarianza asintótica entre 
viene dada por la expresión:
Apéndice D. Estimación de los parámetros π0 y π1
En este apéndice se muestra en detalle la función g(π0, π1; ni, t) utilizada para estimar los parámetros π0 y π1. Esta describe los rendimientos indexados por inflación como funciones cuasicuadráticas de π0 y π1 y permite encontrar sus estimadores mediante la minimización de una suma cuadrática de residuales.
Partiendo de la definición de los rendimientos indexados por inflación, se tiene que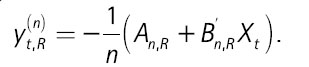 
Reemplazando (18) y (19) en la anterior expresión se puede mostrar que puede escribirse de la siguiente manera:
Nótese que π1 aparece asociado a un término lineal y uno cuadrático, mientras que π0 se encuentra asociado de forma lineal con 
sin depender del vencimiento, lo cual permite interpretarla como la inflación de largo plazo del modelo.
Por tanto, es posible estimar π0 y π1 resolviendo el siguiente problema de optimización:
Es de notar que este problema es equivalente a minimizar la suma de residuales cuadrática 
obtenida a partir del cálculo del proceso iterativo para los rendimientos indexados por inflación descrito en las ecuaciones (18) y (19) sobre estos parámetros.
Por simplicidad en los cálculos se estiman los parámetros a través de la segunda representación, tomando como valor inicial los estimadores de una regresión MCO de la inflación sobre una constante y XtL, siguiendo la forma afín presentada en la ecuación (16).
Apéndice E. Estadísticas descriptivas de los residuales para las recursiones y los excesos de retorno
En este apéndice se presentan algunas estadísticas descriptivas de los errores de valoración para los rendimientos nominales 
reales 
y para el BEI 
, así como los errores de valoración de los excesos de retorno para ambos tipos de rendimiento, respectivamente 
.
Apéndice F. Ajuste de los rendimientos y el break-even inflation
F.1. Rendimientos de los TES en pesos y UVR
A continuación se presentan las figuras correspondientes a los rendimientos nominales e indexados por inflación observados y estimados, con vencimientos de 2, 5 y 8 años.
Figura 4.
Rendimientos observados y estimados de los TES en pesos y UVR para vencimientos a 2 (superior), 5 (medio) y 8 (inferior) años
Figura 4a.
Rendimientos observados y estimados de los TES en pesos y UVR para vencimientos a 2 (superior), 5 (medio) y 8 (inferior) años
Por último, se presenta en la figura 5 el promedio de los rendimientos de los TES en pesos y en UVR observados y estimados por vencimiento.
Apéndice G. Comparación entre B̂gls y Bn obtenido de forma iterativa
En las siguientes figuras se presenta la comparación entre los parámetros Bn y Bn, R + π1 del modelo (ecuación (23)) con respecto a los parámetros Bn y Bn, R + π1 utilizados en la recursión para calcular las descomposiciones de los bonos en ambos casos (ecuación (9) y (19) respectivamente). Estos resultados se muestran para cada uno de los 6 factores.
