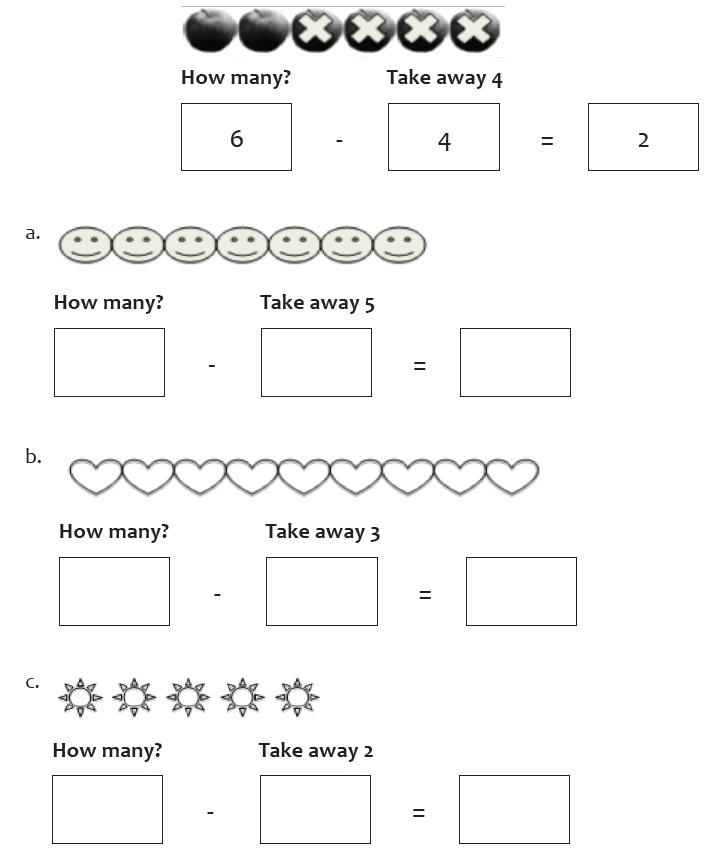
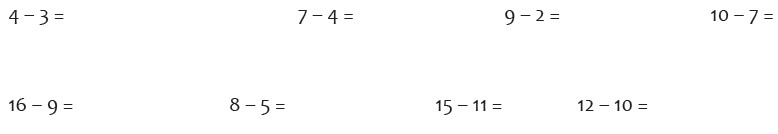Introducción
La experiencia adquirida como docente de matemáticas en inglés con estudiantes que usan el español como lengua materna en instituciones privadas ha generado algunos cuestionamientos relacionados con la manera en que se desarrolla este aprendizaje usando una segunda lengua en el aula. Estos cuestionamientos están relacionados con situaciones que constantemente se presentan en el aula al explicar y desarrollar temas en un idioma que los estudiantes no dominan completamente y que tienen que ver con la necesidad del uso de la lengua materna para lograr el entendimiento y apropiación de los conceptos y procesos que caracterizan el área de las matemáticas en transición del nivel preescolar. Partiendo de este hecho, surgió la necesidad de recurrir al uso de estrategias de enseñanza que fueran de la mano con metodologías inmersas en contextos bilingües y que permitieran desarrollar aprendizajes significativos en los contenidos de matemáticas en situaciones de enseñanza y aprendizaje en inglés.
Adicional a esto, teniendo en cuenta la creciente importancia que en los últimos años ha tenido la educación bilingüe en Colombia, y buscando promover el bilingüismo y multilingüismo para mejorar la enseñanza del inglés y la calidad educativa (de Mejía et al., 2012), destacando la relevancia de la misma dentro del contexto propio de la institución protagonista de la investigación, el hecho de que este tipo de educación permita desarrollar habilidades en dos lenguas y además ganar conocimiento (Krashen, 1997) posibilita la generación de estrategias que abordan la enseñanza de matemáticas en inglés.
Dentro de las políticas bilingües implementadas en algunos contextos educativos, aludiendo al español como lengua materna (L1) e inglés como segunda lengua (L2), se han generado procesos de inclusión, exclusión, estratificación, estandarización y mercantilización de las lenguas extranjeras, hechos que han conllevado situaciones tensas entre los docentes y sus prácticas (Usma, 2009). Atendiendo a una de estas situaciones, como es la tensión protagonizada por los docentes que enseñan matemáticas empleando una segunda lengua, es necesario integrar metodologías a prácticas bilingües que sean coherentes con los procesos de aprendizaje que se dan en asignaturas específicas.
Por lo tanto, el hecho de reconocer que existan métodos de enseñanza bilingües que integran la lengua materna dentro de su propio planteamiento puede permitir el aprovechamiento de la misma para potenciar procesos de enseñanza en matemáticas (citado en de Mejía et al., 2012). Una de estas estrategias es preview-view-review, la cual obedece a tres pasos esenciales: uso de la lengua materna para introducir temas, uso de la segunda lengua para dirigir actividades relacionadas con el tema expuesto, y uso de la lengua materna para resumir ideas principales o hacer preguntas de comprensión (Freeman & Freeman, 2000).
Es así que el problema se observa desde la necesidad del uso del inglés para enseñar matemáticas en cuanto a la información empleada con respecto a conceptos, metodologías y estrategias que caracterizan la educación bilingüe, siendo agravada por la falta de política bilingüe institucional formal ante los docentes, padres de familia y directivos.
Esto dio como resultado la pregunta de investigación: ¿De qué forma la estrategia de enseñanza preview-view-review podría contribuir al aprendizaje de las matemáticas en una segunda lengua en transición? Para dar respuesta se llevó a cabo un estudio en dos grados de transición pertenecientes a un colegio bilingüe femenino de carácter privado en Bogotá (Colombia)1: uno al cual se aplicó la estrategia mencionada (grupo experimental, GE) y otro que mantuvo una estrategia pedagógica tradicional (grupo contraste, GC). Para responder a esta pregunta se acudió al método cuasi experimental de tipo empírico, el cual se caracteriza por la observación y experimentación, enmarcado por la metodología mixta (cuantitativa y cualitativa). Las docentes que participaron en la intervención fueron las directoras de grupo de los mismos y además titulares de las áreas de matemáticas, inglés y ciencias, y la investigadora fue la docente del grupo que recibió la intervención. A continuación se describirán exclusivamente los aspectos que se tuvieron en cuenta para analizar los datos relacionados con la etapa cuantitativa de la investigación.
Marco Teórico
Con el fin de describir algunas metodologías correspondientes a la educación bilingüe es preciso diferenciar los conceptos que se desprenden de esta concepción, como los enfoques, métodos y metodologías de la enseñanza de lenguas:
• Los enfoques: son un conjunto de supuestos sobre la naturaleza de la lengua, su enseñanza y aprendizaje, que se encarga de describir cómo se usa la lengua y cómo sus partes constitutivas se interrelacionan para formar la competencia lingüística (Anthony, 1963, citado en de Mejía et al., 2012, p. 230).
• Los métodos: son la concreción de los enfoques utilizados e involucran la toma de decisiones sobre los tipos de procedimiento, actividades y materiales que conforman el sílabo de instrucción (Harmer, 2001, citado en de Mejía et al., 2012, p. 230).
• Las metodologías: Brown (2001) las define como las prácticas pedagógicas relacionadas con la manera de enseñar o el “cómo enseñar”, que incluye los constructos teóricos y la investigación relacionada (citado en de Mejía et al., 2012, p. 230).
El rol de la L1 en la enseñanza de contenidos académicos en contextos bilingües
Sin pretender estar en pro o en contra de la inclusión o exclusión del inglés como parte del proceso de enseñanza de las matemáticas, existe un propósito implícito en la presente investigación, el cual busca dilucidar el papel que cumple la L1 dentro del marco de la enseñanza de contenidos en inglés, y como se ha descrito anteriormente, una de las intenciones primordiales es presentar algunas concepciones relacionadas con este aspecto, que servirán de fundamentación teórica para construir las reflexiones a partir de los resultados que arroje la investigación.
Además, el hecho de involucrar estas prácticas en edades tempranas permite reconocer debilidades y fortalezas, con el fin de realizar programas específicos para cada niño, a fin de potenciar de esta manera su desarrollo (de Mejía, 2012). En otras palabras, como mencionan Genesee, Nicoladis & Paradis (1995) y Bauer (2000), mientras los niños están aprendiendo una segunda lengua, la lengua materna es la base para que las habilidades de una se transfieran a la otra y, por lo tanto, se pueda emplear en la enseñanza de un contenido académico, además de involucrar un propósito comunicativo, lo cual en estas edades es básico para crear motivación y entendimiento (citados en Robles, 2010).
Vale la pena tener en cuenta el principio de complementariedad adoptado por Grosjean (2010), el cual manifiesta que las personas bilingües adquieren y usan sus lenguajes para diferentes propósitos en diversos dominios de la vida con distintas personas; en síntesis, los diferentes aspectos de la vida frecuentemente requieren diferentes lenguajes. Este principio sirve como base estructural de este marco conceptual, dado que la persona bilingüe no se desarrolla igual, ya que depende del contexto en que se encuentre, de manera tal que impacta en el uso de las lenguas de acuerdo con la necesidad, y para este caso particular, el contexto se refiere a las clases de matemáticas en un ambiente bilingüe.2
El investigador Cummins (2001) indica las ventajas del bilingüismo dentro de los procesos lingüísticos de los niños y menciona el impacto positivo que conlleva el fomento de la lengua materna en el aula para el desarrollo de la segunda lengua en contextos académicos, a propósito de la prevención que algunos educadores y padres de familia puedan tener con respecto al efecto negativo que el uso de la L1 pueda tener en la L2, teniendo en cuenta que esta propuesta trata de la aplicación de la estrategia preview-view-review en un contexto bilingüe. Esto no quiere decir que al atender a la L1, para efectos académicos en la L2, se pueda o se deba usar indiscriminadamente la L1; lo que se pretende es adoptar una metodología que permita aprovecharse de la lengua materna en función del contenido matemático, acudiendo a técnicas como la anteriormente mencionada.
Se encuentra pertinente considerar dos convenciones propuestas por Jarrett (1999) en relación con los lenguajes manejados en el aula de clases. 1. El lenguaje social, que es definido como aquel que permite a los estudiantes que usan la L1 inferir significado e interpretar el lenguaje corporal y visual, el cual se construye de manera colaborativa. 2. El lenguaje académico, que es más abstracto y contiene palabras más especializadas. En este caso, los estudiantes son responsables de construir significados de manera individual, confiando en su propio entendimiento, tanto de la lengua como de los conceptos involucrados, permitiendo que los dos lenguajes sean importantes para el desarrollo social y de aprendizaje de los estudiantes, y relativamente competentes en el aspecto social, mientras que el académico debe ser enseñado explícitamente (Kang y Pham, 1995; Laplante, 1997; Lee y Fradd, 1996, citados en Jarrett, 1999).
Teniendo en cuenta esta distinción, Jarrett (1999) además menciona que a pesar de los variados debates centrados en establecer qué lengua debería ser usada para enseñar contenidos, si la L1 o L2, algunos estudios demuestran que la L1 tiene un papel importante en el aprendizaje de las matemáticas y ciencias. Kang y Pham (1995) y Latham (1998) manifiestan que cuando se les permite a los estudiantes usar la L1 en el aula, generalmente mejora el desempeño académico de éstos en las dos áreas; por lo tanto, como menciona Cummins (1992, citado por Rupp, 1992), sería favorable para estudiantes menores usar la L1 para el lenguaje académico porque les permite construir bases a partir de los conceptos de matemáticas y/o ciencias, antes de entrar a grados superiores donde el idioma se convierte en algo más descontextualizado y demandante cognitivamente (citados en Jarrett, 1999).
En la misma línea, Crawford (1995) menciona que las habilidades en áreas de contenido como las matemáticas y estudios sociales, una vez aprendidas en L1, se mantienen cuando la instrucción cambia a la L2 (citado en Jarrett, 1999). Lo anterior es apoyado por Silva y Simonsen (2007), ya que algunos estudios han comprobado que impartir aritmética en una lengua distinta a la materna puede complicar el aprendizaje.
Estrategias que involucran la L1 en un contexto bilingüe
Considerando que enseñar matemáticas en clases multilingües, por ejemplo, requiere especial cuidado en el uso lingüístico empleado (Barwell, 2002, 2005a, 2005b; Frederickson & Cline, 2002, citados en de Mejía et al., 2012), es importante determinar las estrategias que pueden beneficiar los aprendizajes en matemáticas, de acuerdo con el contexto del colegio, reconociendo el hecho de que esta área ya usa el inglés como medio de instrucción. Aunque existen varias estrategias en este campo, se tendrá en cuenta solamente la técnica preview-view-review, ya que fue la que protagonizó la intervención y permitió hacer la comparación entre los grupos de manera cuantitativa, que es a lo que este artículo se refiere.
Como ya se mencionó, la estrategia pedagógica llamada preview, view, review (Freeman & Freeman, 2000) está determinada por “una relación interactiva y secuencial entre las dos lenguas del aprendiz, a fin de asegurar un desarrollo cognitivo y lingüístico óptimo” (de Mejía & Fonseca, 2009, p. 87). Esta estrategia, la cual puede ser aplicada por uno o dos docentes, plantea tres etapas, que se presentan en la tabla 1, tomando en cuenta la descripción hecha por de Mejía y Fonseca (2009):
Tabla 1.
Descripción de la estrategia preview-view-review
De acuerdo con Freeman y Freeman (2000), dicha estrategia favorece el entendimiento de los procesos matemáticos en un contexto bilingüe y ayuda a los docentes a evitar la traducción recurrente generando motivación en los estudiantes. Adicionalmente, existe un estudio similar hecho en Cali (Marulanda, 1995) con alumnos de cuarto de primaria, el cual arrojó resultados positivos en la asimilación de conceptos matemáticos y de L2 al usar dicha estrategia.
Metodología
Con el fin de determinar de qué manera la estrategia de enseñanza descrita previamente pudo, o no, contribuir al aprendizaje significativo de las matemáticas en el nivel de transición en un colegio privado de Bogotá, el diseño de investigación al que se recurrió se basó en el diseño cuasiexperimental de tipo empírico, el cual se caracteriza por la observación y experimentación, enmarcado por la metodología cuantitativa y cualitativa (Bisquerra, 1989). Para propósitos específicos de este artículo, sólo se describirán el componente cuantitativo y las conclusiones arrojadas por las pruebas de aprendizaje, las cuales determinaron el uso de datos que fueron analizados de manera cuantitativa.
De esta manera, teniendo en cuenta sólo la etapa cuasiexperimental, la cual requirió un grupo contraste (Morales, 2013) y otro experimental, se consideró la aplicación de la prueba estadística llamada Mann Whitney, que hace parte del programa SPSS, con el fin de comparar el desempeño de los dos grupos antes, durante y después de la intervención. Por lo tanto, siguiendo la línea Sampieri (2003), esta metodología de tipo cuantitativo “usa recolección de datos para probar hipótesis con base en la medición numérica, y análisis estadístico para establecer patrones de comportamiento” (p. 10).
Para llegar a la toma de decisión del uso de la prueba no paramétrica de Mann Whitney, la cual “es considerada la más potente para comparar 2 variables diferentes continuas independientes” (Vega y Sánchez, 2008, p. 6), se pensó realizar un estudio de normalidad, ya que, siguiendo la línea de Figueras y Gargallo (2003), para que las variables tengan una mayor validación es preciso comprobar la normalidad en la distribución de los datos, lo cual se puede dar contrastando las hipótesis por medio del test de Shapiro y Wilks, el cual es utilizado para muestras pequeñas, como en este caso, por estar trabajando con grupos de 23 y 24 estudiantes.
Con el fin de determinar si la técnica preview-view-review generó o no un impacto positivo en el aprendizaje de las matemáticas se administraron tres pruebas de aprendizaje como métodos de recolección de datos y un mismo test, que se efectuó al final y al principio de la intervención. Es importante mencionar que como parte complementaria de la investigación se incluyeron observaciones y grabaciones (en video) de clase en los dos grupos mencionados, diseño de actividades, diario de campo y entrevistas con docentes, jefe de Departamento de Inglés y de Matemáticas, coordinador académico y rectora, lo cual hizo parte de la etapa cualitativa de la investigación, y que no se presentará en este documento, pero que, así como lo menciona Pereira (2011) haciendo alusión al tipo de diseño con modelo mixto, reconoce que de manera simultánea se exploren y se confirmen datos a partir de análisis cuantitativos y cualitativos, lo que “permite una mayor comprensión del objeto de estudio” (p. 20), lo que se logró por medio de la triangulación de datos.
Contexto
El lugar en el que se realizó la intervención es un colegio femenino de carácter privado ubicado en Bogotá. Esta institución de calendario B (donde el año escolar comienza a mediados de agosto o a principios de septiembre y finaliza a mediados de junio) se destaca por mantener un nivel académico superior y una educación bilingüe satisfactoria, la cual se inicia desde los primeros grados del preescolar. Los niveles que pertenecen a esta sección del colegio se dividen en pre-jardín, jardín, transición y primero, y el número de estudiantes oscila entre 23 y 26 niñas por curso.
Como ya se mencionó, la institución actualmente está atravesando por un momento de transición en algunos de sus currículos y políticas institucionales. Como parte de estos cambios se encuentra la política de lengua, la cual está en proceso de construcción, lo que significa que hasta el momento el colegio no cuenta con parámetros establecidos para la enseñanza de contenidos en inglés, y por lo tanto las docentes no tienen lineamientos específicos del manejo de la lengua materna en el aula. Adicional a esto, el programa de matemáticas está llevando un proceso de evaluación, teniendo en cuenta que hace tres años se adoptó el método natural (Díez, Pantano, Camargo, 2012), el cual ha modificado prácticas docentes y estructuras curriculares.
Estudiantes
Los grupos de estudiantes los conformaron niñas entre los 6 y 7 años de edad, y se caracterizaron por tener niveles académicos similares, ya que, como parte de los objetivos de cada área, es indispensable que tanto las docentes como las estudiantes de cada nivel den cuenta de los mismos logros académicos durante el año. Esto se evidencia por medio de las evaluaciones y los reportes académicos hechos en cada período escolar, para ser discutidos en reuniones semanales y poder tratar casos particulares, con el fin de hacer seguimientos de estudiantes con terapias ocupacionales, psicología, fonoaudiología, tutorías y otras ayudas externas. Para este caso en particular se logró determinar que las estudiantes del grupo contraste tenían un mejor desempeño tanto en matemáticas como en inglés, gracias a los reportes académicos que hasta el momento habían arrojado las estudiantes.
Docentes
La profesora del grupo experimental, como ya se mencionó, fue la docente investigadora, la cual es especialista en lenguas, y su experiencia laboral se ha mantenido en los niveles de preescolar y primaria por trece años (como profesora de inglés en varios niveles de escolaridad y de matemáticas por seis años en primaria). Esta docente inició la licenciatura en Matemáticas en 1996, pero después de un año abandonó la carrera para estudiar la licenciatura en Filología e Idiomas. Esa oportunidad preliminar de estudio le permitió acceder a esta área del conocimiento desde la docencia en los niveles antes mencionados, y se ha mantenido actualizada en temas de didáctica de la matemática desde entonces.
La profesora del grupo contraste, quien accedió a participar en la intervención de manera voluntaria, es especialista en Educación Preescolar, por lo que su experiencia se ha basado en estos niveles específicamente durante dieciséis años. Esta docente adquirió la segunda lengua durante su período de escolaridad en el colegio y la universidad. Su experiencia como docente de matemáticas inició desde el momento en que empezó su vida laboral en los niveles de preescolar y primaria, y ha procurado estar actualizada por medio de diferentes capacitaciones en cada lugar de trabajo. Su preparación en cuanto a la materia estuvo inmersa dentro de la licenciatura y la especialización que tiene la docente con relación a la educación preescolar y a los procesos de pensamiento de los niños.
Descripción de la Intervención
Las clases que se realizaron en los dos grupos durante el tiempo de la intervención fueron aproximadamente 30 horas de 40 minutos, del 21 de abril al 7 de junio de 2014. Antes de iniciar la primera fase se aplicó un pre test de cinco preguntas de seis ejercicios aproximadamente en cada una, el cual duró dos sesiones. La primera etapa (preview) se dio durante cuatro sesiones, en las cuales se manejó la lengua materna para introducir el tema en el GE. La segunda etapa (view) fue la más prolongada, alrededor de dieciséis sesiones, en donde se desarrollaron en segunda lengua las actividades mencionadas anteriormente, que incluyeron el reconocimiento de situaciones que implicaban resta, identificación de símbolo, realización de operaciones sencillas con números del 1 al 20 (cálculo mental) y resolución de problemas, y en la que se realizaron dos pruebas de aprendizaje. La etapa final (review) se desarrolló en lengua materna durante tres sesiones, en las que se retomaron conceptos, definiciones y ejercicios que atendieron a la secuencia didáctica que se siguió y a los desempeños planeados, y en la que se realizó una evaluación final. Al finalizar la intervención, las estudiantes del GE y GC contestaron el post test en una sesión de 40 minutos. El GC tuvo la misma secuencia del proceso de enseñanza-aprendizaje que tuvo el GE, pero todo se desarrolló en segunda lengua.
En la tabla 2 se presentan de manera detallada los momentos de diseño, corrección y validación de algunos instrumentos de recolección de datos que se aplicaron durante la intervención, lo cual se describe por etapas para cada uno de los instrumentos que requirieron varios rediseños por parte de la investigadora.
Tabla 2.
Etapas para validación de algunos instrumentos de recolección de datos
Pre test
Para iniciar la intervención se diseñó un examen relacionado con la planeación y ejecución de las actividades características de la ruta didáctica que la institución ha creado para cada área, el cual mantuvo conexión con la metodología y los desempeños para el tercer trimestre del año escolar, con el fin de conocer qué tanto las estudiantes de transición estaban familiarizadas con el concepto de resta (ver anexos).
El primero de estos aspectos respondió a una metodología que promueve la construcción del pensamiento partiendo del estudiante como eje principal del proceso de aprendizaje. Los desempeños atendieron a lo que se esperaba que las estudiantes lograran al final del trimestre en el pensamiento numérico, los cuales fueron preestablecidos de acuerdo con el nivel de las estudiantes en el momento de la planeación de los mismos, y los cuales permitieron construir la ruta didáctica que se siguió durante el proceso de enseñanza de noción de resta.
Durante el proceso, este examen tuvo cuatro modificaciones, que se dieron de acuerdo con el resultado de los pilotajes que se realizaron de cada una de las versiones. Estas modificaciones tuvieron que ver con el tipo de pregunta, el vocabulario, las imágenes y la complejidad en los problemas. Adicionalmente, el examen dio cuenta de las etapas que las estudiantes debían recorrer y reconocer durante el proceso de aprendizaje en este contexto específico, y, por lo tanto, el acompañamiento por parte de la jefe del Departamento de Matemáticas fue fundamental para que el examen cumpliera con los parámetros establecidos por la institución con respecto a contenidos, forma de evaluar, relación entre desempeños, objetivos y formato.
Finalmente se aplicó el examen a los tres cursos de transición, el cual se basó en el siguiente desempeño: la estudiante es capaz de reconocer el concepto de resta por medio de situaciones cotidianas de manera estratégica, con los siguientes indicadores de desempeño: soluciona situaciones diversas por medio del reconocimiento de la noción de resta; establece diferencias entre situaciones que involucran suma y resta; resuelve situaciones cotidianas usando el proceso mental de la resta (ver la tabla 3).
Después de obtener los resultados de esta prueba se establecieron los grupos de trabajo para iniciar el diseño de las actividades llevadas a cabo en cada una de las etapas de la intervención.
Actividades: etapa preview
Durante esta etapa, la noción de resta fue introducida por medio de un cuento que hablaba de animales que se querían ir a dormir, el cual sirvió de abrebocas para que las estudiantes tuvieran la posibilidad de hablar de lo que estaba pasando e inferir la situación principal con la ayuda de la docente para llegar al término de resta (substraction). Después, las profesoras crearon diferentes situaciones problema relacionadas con la vida cotidiana para que las estudiantes buscaran la manera de resolverlas, atendiendo a lo que su imaginación y sus conocimientos previos les permitieran. Se acudió luego al uso de material concreto para representar situaciones numéricas sencillas, para pasar después al semi-concreto.
Aparte de la L1 y L2 como factores diferenciadores de la intervención en cada grupo, la intensidad de las actividades de práctica en el GC fue mayor, ya que la docente invirtió más tiempo en la lectura del cuento y de las situaciones problema que la docente del GE, hecho que será analizado en la presentación de los resultados.
Actividades y pruebas de aprendizaje: etapa view
En esta etapa se desarrollaron diferentes actividades basadas en el juego y en el contexto de las estudiantes, en el momento de desarrollar situaciones problema. Las clases generalmente se iniciaron con ejercicios simples de cálculo mental y/o videos que pretendieron crear una atmósfera agradable y motivacional para las estudiantes, con el fin de ambientarlas en el tema nuevo de resta.
Se realizó también una tienda, en la que las estudiantes cumplieron los roles de compradoras y vendedoras, con el fin de realizar operaciones sencillas basadas en una actividad de recreación, imaginación y movimiento.
Para esta fase se aplicaron dos pruebas de aprendizaje, con el fin de reconocer las fortalezas y debilidades que las estudiantes tenían con respecto al reconocimiento de las situaciones que representaban resta, identificación del símbolo, operaciones simples y resolución de problemas. Cada una de las pruebas fue piloteada dos veces y tuvo el seguimiento y acompañamiento de la jefe del Departamento de Matemáticas.
Actividades y pruebas de aprendizaje: etapa review
Ésta fue la última etapa de la técnica planteada para la intervención, en la cual se realizaron actividades similares a las que se aplicaron en la etapa previa, pero con la diferencia que en el GE la lengua materna fue empleada para retomar dudas de las estudiantes a partir de ejercicios planteados por ellas mismas, mientras que la docente en el GC continuó usando la segunda lengua, con el mismo propósito. Durante esta fase también se aplicó un examen que tuvo la característica de manejo de lengua diferente (GE en L1 y GC en L2), el cual buscó revaluar y cerrar los conceptos básicos que las estudiantes supuestamente debían manejar para ese momento, como el manejo del símbolo, la resolución de problemas, la identificación de representaciones gráficas de suma y resta y operaciones mentales sencillas.
Post test
En esta etapa se aplicó el mismo test que se realizó al principio de la intervención, con dos propósitos básicos. El primero, con el fin de establecer comparaciones entre el desempeño de cada grupo al inicio y finalización de la intervención, y el segundo tuvo que ver con la evaluación formal de finalización de desempeño.
A propósito de esto último, en el nivel de preescolar de la institución se maneja la evaluación formativa para dar cuenta de los procesos en cada una de las materias a partir del desarrollo de competencias y habilidades de acuerdo con las edades, los desempeños y contenidos planeados por cada departamento. Por lo tanto, la valoración, la cual va de una a cuatro estrellas, se da de forma procesual y descriptiva para cada una de las estudiantes, a partir de actividades individuales, de acuerdo con criterios establecidos por el equipo de profesoras de transición.
Aprovechando el tipo de evaluación que la institución maneja, se realizaron los tres exámenes anteriormente descritos, para valorar cada uno de los indicadores y etapas de la ruta didáctica.
Resultados
De acuerdo con la pregunta de investigación que busca responder a la manera en que la estrategia de enseñanza preview-view-review puede contribuir a la comprensión de conceptos y procesos matemáticos en transición, se presenta la descripción de los resultados encontrados, después de haber codificado y categorizado los datos recogidos en las diferentes pruebas realizadas.
Para efectos de clasificación, se manejarán las siguientes convenciones, que atienden a los diferentes participantes en la investigación:
• Docente investigadora: I
• Docente grupo contraste: docente M
• Grupo contraste: GC
• Grupo experimental: GE
Antes de presentar los resultados que emergieron de la comparación de los dos grupos y del análisis del contexto de trabajo es necesario exponer la manera en que se manejaron los datos del pre test para elegir al grupo contraste, además de entrar en comparación con el post test.
En la gráfica 1 se indica que los cursos TRA y TRC no tienen una distribución normal de los datos, ya que TRA muestra dos datos atípicos, y TRC uno, mientras que TRB sí mantiene una normalidad y presenta la media más alta entre los tres cursos.
Fue por esta razón que se decidió hacer la intervención con los grupos de TRA (GC) y TRC (GE), ya que estos dos cursos presentaron características similares en cuanto a los resultados arrojados por el pre test, siendo TRC el grupo que manejó la docente investigadora. Es por esta razón que el diseño de investigación atendió a un manejo cuasiexperimental, por el hecho de no haber escogido el grupo de manera aleatoria (Sampieri, 2003).
Comportamiento de la L1 y L2 durante la intervención
Se hace referencia a esta subcategoría, ya que el desarrollo del tema, noción de resta, implicó usar actividades que requirieron el manejo por parte de las estudiantes de las habilidades de escucha y lectura en los dos idiomas, aunque la parte oral, como ya se describió, se dio de manera más flexible. Teniendo en cuenta que la intervención se realizó al finalizar el año escolar, se pudo evidenciar que las estudiantes tenían un mejor manejo tanto de la lengua materna como de la segunda lengua, y de esta manera, la exigencia era mayor en todas las habilidades de los idiomas, haciendo alusión a los dos grupos, ya que tanto los procesos de adquisición de lengua como los de desarrollo de pensamiento en matemáticas involucran un trabajo conjunto de las docentes participantes en la investigación, permitiendo que las dos reconozcan este seguimiento desde el inicio del año escolar.
De acuerdo con esto, las pruebas escritas se caracterizaron por tener las instrucciones escritas de una manera sencilla para las niñas, teniendo en cuenta expresiones que para las estudiantes fueran familiares, y aunque algunos problemas fueron apoyados con imágenes, siempre se escribieron explícitamente, y las estudiantes también debieron seguir las instrucciones de las docentes para dar solución a cada ejercicio.
Es necesario entonces acudir a los resultados que se obtuvieron en las pruebas que se realizaron en cada una de las etapas, con el fin de analizar la comprensión de la L2, teniendo en cuenta que los dos grupos tuvieron características similares en el pre test, el cual se abordará más adelante de una manera detallada, junto con el post test. Antes de hacer referencia a los resultados, es preciso mencionar que para las tres evaluaciones realizadas fue necesario aplicar una prueba para verificar si los datos presentaban una normalidad en su distribución, con el fin de establecer el tipo de comparación. Para los tres casos, no hubo distribución normal de la información, lo cual sugirió usar la prueba de Mann Whitney, con el fin de comparar el desempeño de los dos grupos en las evaluaciones realizadas durante la intervención.
En la etapa view se aplicaron dos pruebas en inglés, con el propósito de verificar y evaluar los contenidos que se habían trabajado hasta el momento. La primera evaluación consistió en el reconocimiento y la diferenciación entre situaciones gráficas y numéricas que representaban suma y resta (ver anexos). Se diseñaron diez ejercicios, que tuvieron como característica fundamental las imágenes o situaciones que podrían representar resta, con el equivalente numérico. Teniendo en cuenta las edades de las estudiantes, el hecho de haber empezado con representaciones gráficas les permitió manejar, de manera concreta, la noción de este concepto, atendiendo a la sugerencia hecha por la docente A, durante el acompañamiento de las planeaciones de clase.
En términos numéricos, el promedio arrojado para GC fue de 7,46, con 20 estudiantes con un puntaje mayor que 6 (24 estudiantes en total), y para GE fue de 7,43, con 14 estudiantes con puntaje mayor que 6 (23 estudiantes en total).
La tabla 4 evidencia que en esta primera evaluación no hubo una diferencia significativa entre las medias de los dos grupos, de acuerdo con el valor de significancia resaltado. El desempeño en general fue bueno; sin embargo, como docentes se esperó que éste fuera mucho mayor, por tener representaciones gráficas y manejar solamente instrucciones de manera oral.
Tabla 4.
Comparación entre los GE y GC en la evaluación 1
| EVALUACIÓN 1 | |
|---|---|
| U de Mann-Whitney | 270,000 |
| W de Wilcoxon | 570,000 |
| Z | -,130 |
| Sig. asintótica (bilateral) | ,897 |
Teniendo en cuenta que en el GC cuatro niñas obtuvieron menos de seis respuestas correctas, y en GE nueve niñas, se podría afirmar que el GE continuaba caracterizándose por tener un desempeño bajo, mientras que el GC permanecía con mejores resultados, así como se mostró anteriormente en el pre test. Sin embargo, se podría deducir de los resultados de esta evaluación que el GE mejoró en su desempeño, ya que al iniciar la intervención fue el grupo que obtuvo el promedio más bajo en el pre test, y al responder la primera evaluación, su desempeño fue prácticamente igual al del GC.
Por otra parte, la segunda evaluación (ver anexos) tuvo por objetivo evaluar los tres indicadores de desempeño y determinar el progreso de las estudiantes en cuanto al manejo del concepto de resta, para dar cuenta de las notas del trimestre. Para esta prueba se diseñaron diez ejercicios, que se caracterizaron por tener representaciones numéricas, gráficas y problemas simples. El promedio de GC fue de 7,13 con siete estudiantes con desempeño bajo, es decir, por debajo de 6, y ocho estudiantes obtuvieron 9 puntos, y un estudiante 10 puntos (23 estudiantes en total), mientras que en el GE el promedio fue de 8,30, con cuatro niñas por debajo de 6 respuestas correctas, seis niñas obtuvieron puntaje de 9, y siete niñas lograron tener 10 respuestas correctas (23 estudiantes en total) (ver la tabla 5).
Tabla 5.
Comparación de los GE y GC de la evaluación 2
| EVALUACIÓN 2 | |
|---|---|
| U de Mann-Whitney | 180,500 |
| W de Wilcoxon | 480,500 |
| Z | -2,078 |
| Sig. asintótica (bilateral) | ,038 |
En este caso, el GE tuvo una diferencia significativa con el GC, de acuerdo con el valor resaltado, lo que podría significar que un 82,60% de las estudiantes logró los objetivos propuestos para ese momento, mientras que en el GC el 69,56% aprobó el examen con más de seis respuestas correctas.
Adicional a esto, se evidenció una mejora en el desempeño de las estudiantes del GE de la primera prueba a la segunda, mientras que el GC tuvo una leve disminución en el promedio, y el número de estudiantes con promedio bajo creció. Esto se pudo presentar porque el examen requirió más trabajo por parte de las estudiantes en términos de tiempo, número de instrucciones y tipo de pregunta, ya que en esta ocasión, además de relacionar situaciones gráficas con números, las estudiantes realizaron operaciones mentales simples y resolvieron problemas sencillos, lo que podría significar que el GE tuvo una mejor comprensión de las instrucciones dadas de manera oral, y aunque los problemas no los pudieron leer de manera individual, hicieron un seguimiento a la lectura de ellos con la compañía de la docente en repetidas ocasiones.
Finalmente, la tercera evaluación se realizó al final de la intervención, en la etapa de review, lo que llevó a su aplicación en lengua materna para el GE (ver la tabla 6). Esta evaluación tuvo como objetivo primordial evaluar a las estudiantes en la resolución de problemas, aprovechando que el pre test demostró que en este tipo de ejercicios (complementándolos con gráficas), las estudiantes tuvieron mejor desempeño. Los problemas fueron presentados representando un grado de dificultad, siendo el primero más sencillo que los últimos dos, con cinco ejercicios en total.
El promedio que tuvo el GC fue 3,42 con once estudiantes que tuvieron un desempeño básico, es decir, menor o igual a 3 ejercicios correctos, lo que representó un 54% de estudiantes con un puntaje mayor o igual que 4, mientras que el GE tuvo 4,43, con dos estudiantes con desempeño básico, lo que representó un 91,3% de estudiantes con un puntaje mayor o igual que 4.
Tabla 6.
Comparación de los GE y GC en la evaluación 3
| EVALUACIÓN 3 | |
|---|---|
| U de Mann-Whitney | 129,500 |
| W de Wilcoxon | 429,500 |
| Z | -3,287 |
| Sig. asintótica (bilateral) | ,001 |
En esta prueba se evidenció también una diferencia significativa entre las medias de los dos grupos, de acuerdo con el valor resaltado, y un incremento de la segunda prueba a esta última en el GE, en términos de las estudiantes que venían presentado desempeño bajo. Adicional a esto, teniendo en cuenta que el problema 5 representó mayor grado de dificultad, fue claro que un número importante de estudiantes lo logró solucionar, 13 en el GE y 4 en el GC.
El hecho de haber empleado la lengua materna para la realización y ejecución de esta prueba pudo haber permitido que las estudiantes siguieran la lectura de las instrucciones y de los problemas, simultáneamente con la docente, un entendimiento claro de lo que se pretendía resolver, y además acudir a una segunda lectura, si la estudiante lo consideraba necesario.
Se mostró entonces que a medida que pasaba el tiempo se notaba un incremento en el desempeño del GE en términos de las medias, las cuales fueron de 7,4/10, 8,3/10 y 4,4/5, mientras que el GC extrañamente demostró una disminución de las mismas: 7,4/10, 7,1/10 y 3,4/5.
Desempeño de las estudiantes antes y después de la intervención
Esta última categoría da cuenta de los resultados que las estudiantes obtuvieron al iniciar y finalizar la intervención, y la relación que el desempeño de cada grupo podría tener teniendo en cuenta al análisis previo en cada categoría.
Para el pre test, el resultado que se obtuvo al aplicar la prueba de Mann Whitney se muestra en la tabla 7.
Tabla 7.
Comparación entre el GE y el GC en el pre test
| PRE TEST | |
|---|---|
| U de Mann-Whitney | 191,000 |
| W de Wilcoxon | 467,000 |
| Z | -1,824 |
| Sig. asintótica (bilateral) | ,068 |
De acuerdo con el valor resaltado, no hubo diferencias estadísticamente significativas entre los dos grupos al inicio de la intervención, lo cual pudo indicar una ventaja para comenzar a aplicar la estrategia mencionada en el grupo experimental, ya que en general, al no encontrar diferencias significativas, se pudo partir de dos grupos que guardaban similitudes con respecto a la aproximación de la noción de resta. Sin embargo las estudiantes del GC tuvieron mejor promedio que el GE (ver la tabla 8).
Tabla 8.
Medias de los GE y el GC en el pre test
| GRUPO INICIAL | Estadístico | ||
|---|---|---|---|
| PRE TEST | GE | Media | 5,21 |
| Mediana | 4,00 | ||
| GC | Media | 3,30 | |
| Mediana | 3,00 | ||
De acuerdo con el número de preguntas totales, se observa un promedio bajo para los dos grupos, y se puede considerar que las estudiantes, en su gran mayoría, para ese momento no reconocían situaciones que representaban resta, de manera gráfica y simbólica, aunque las situaciones problema las entendieron más, muy seguramente debido al nivel de inglés que manejaban en ese entonces. Es decir, aparentemente la habilidad de escucha en la segunda lengua les permitió resolver problemas con más facilidad que otro tipo de ejercicios que requirieron una ejecución relacionada con la noción netamente de resta.
Para el propósito de la presente investigación, fue interesante haber encontrado que el GE haya arrojado resultados más bajos en el pre test que el de contraste, lo cual hizo que se reforzara la intención de la propuesta al aplicar una estrategia que involucrara la lengua materna al enseñar matemáticas en un contexto bilingüe en preescolar.
Con respecto a los resultados obtenidos en el post test para los dos grupos, a continuación se presenta la prueba de normalidad a los que fueron sometidos, con el fin de determinar si los datos tenían una distribución normal o no.
En los dos grupos los datos no tienen una distribución normal (ver la gráfica 2), ya que hay estudiantes que están por fuera de la media, demostrando un desempeño más bajo en esta prueba.
Teniendo esta desviación en cuenta, se acudió a la prueba de Mann Whitney para determinar si al final de la intervención las estudiantes tuvieron diferencias significativas en su desempeño con respecto al reconocimiento y aplicación de la noción de resta. La tabla 9 muestra dicha información.
Tabla 9.
Comparación entre el GE y el GC en el post test
| POSTEST | |
|---|---|
| U de Mann-Whitney | 107,500 |
| W de Wilcoxon | 407,500 |
| Z | -3,632 |
| Sig. asintótica (bilateral) | ,000 |
De acuerdo con el valor de significancia resaltado, se pudo determinar que sí hubo diferencias significativas al comparar los resultados del post test de los dos grupos al terminar la intervención, lo que permite deducir que la estrategia preview-view review tuvo un impacto positivo y estadísticamente significativo en el desempeño de las estudiantes con respecto al manejo y reconocimiento de la noción de resta.
Adicional a esto, se puede evidenciar la diferencia entre las medias de los dos grupos, las cuales representan un incremento significativo en comparación con el promedio obtenido en el pre test (ver las tablas 10 y 11).
Tabla 10.
Comparación de medias de los GC y GE en el post test
| GRUPO FINAL | Estadístico | ||
|---|---|---|---|
| POST TEST | GC | Media | 25,92 |
| Mínimo | 10 | ||
| Máximo | 29 | ||
| GE | Media | 28,39 | |
| Mínimo | 21 | ||
| Máximo | 31 | ||
Tabla 11.
Desviación estándar
Las tablas 10 y 11 describen estadísticamente las diferencias que los dos grupos tuvieron al finalizar la intervención, en el resultado del post test. Entre las dos medias hubo una diferencia de 2,47, en donde el valor mínimo fue de 21 puntos en el GE, mientras que en el GC fue de 10. Adicional a esto, en el GE hubo estudiantes con el puntaje máximo, hecho que no se presentó en el GC.
Se evidencia entonces un buen desempeño por parte de los dos grupos en post test, lo que significa que las estudiantes lograron, en su mayoría, los objetivos propuestos al inicio de la intervención. Sin embargo, teniendo en cuenta los promedios de los dos grupos en esta prueba, el GE obtuvo un mayor promedio que el GC, lo que ya demostró que la estrategia aplicada permitió que el desempeño de las estudiantes de este grupo fuera significativamente mayor que el del GC. Adicional a esto, se pudo evidenciar también que el valor mínimo que obtuvo una estudiante del GE fue de 21 puntos, mientras que en el GC fue de 10, lo que también representó un desempeño alto en aquella estudiante con posibles dificultades de aprendizaje, en el GE.
Conclusiones, Implicaciones y Limitaciones
Este capítulo presenta las conclusiones que se pudieron deducir de la descripción cuantitativa de los resultados, las cuales están fundamentadas teóricamente de acuerdo con lo reflejado en el contexto analizado. Básicamente, estas reflexiones se centraron en responder a la pregunta de investigación, que evidencian cómo la estrategia de enseñanza preview-view-review contribuyó al desempeño de las estudiantes en la comprensión de conceptos y procesos matemáticos relacionados con la noción de resta. Finalmente se expondrán algunas implicaciones como consecuencia de las conclusiones presentadas.
Atendiendo a la lectura de los resultados obtenidos a partir de la prueba de Mann Whitney, se puede concluir que hubo una diferencia estadísticamente significativa entre los desempeños de los dos grupos al final de la intervención, ya que el valor de significancia que arrojó esta prueba fue menor de 0,05, lo que evidenció que la estrategia aplicada permitió que las estudiantes tuvieran un mejor manejo de los contenidos matemáticos, encontrando relación con lo que menciona Brice (2001), quien cita a Vigotsky (1962) con respecto a la ventaja de poder expresar el mismo pensamiento en más de una lengua, lo que permite al niño comparar y contrastar los dos sistemas conllevando una mayor conciencia cognitiva y metalingüística. Esto se cita a propósito de la sección review, en la cual se retomaron y se aclararon conceptos y situaciones en lengua materna.
Entonces, de una u otra manera se pudo comprobar la presunción que desde un principio motivó esta investigación, a propósito de las implicaciones y los beneficios que traería la aplicación estrategia preview-view-review en este contexto, lo cual sirve como base para establecer las subsiguientes reflexiones.
Adicional a esto, y retomando lo que la institución vio al inicio como desventaja al aplicar una estrategia que involucraba la L1 en un contexto bilingüe, se pudo deducir que el atraso que se pensó podía ocurrir en la segunda lengua no sucedió, debido a que el post test y dos de las tres evaluaciones fueron aplicados en L2, y las estudiantes del GE tuvieron un desempeño alto manejando también el vocabulario y expresiones característicos del tema.
Igualmente, así como se evidenció en el estudio hecho por Marulanda (1995) en Cali con respecto a los estudiantes con bajo rendimiento académico, este estudio también ratificó dicha formulación, puesto que en el GE el valor único más bajo en el post test fue de 21 puntos sobre 31, hecho que demuestra que haber usado la lengua materna en el aula benefició a las estudiantes que se habían destacado durante el año por haber tenido bajo nivel académico en matemáticas.
Aprovechando que la estrategia preview-view-review demostró resultados positivos en el desempeño numérico al finalizar el año escolar en transición, cuando las estudiantes habían alcanzado un nivel de lengua más consolidado, valdría la pena recurrir a esta práctica para la enseñanza del contenido matemático en las edades más tempranas, en donde han acabado de salir de su período silencioso (pre-jardín) y han entrado a una etapa (jardín) donde empiezan a adquirir más vocabulario y herramientas que van estimulando cada habilidad, de acuerdo con la edad.
En contraste, también se podría analizar la aplicación de la estrategia en niveles más avanzados de la L2. Si bien Marulanda (1995) tuvo resultados similares habiendo aplicado la técnica en un contexto bilingüe en Cali en cuarto grado, podría ser significativo o no el hecho de recurrir a la lengua materna reconociendo que los estudiantes ya tengan la segunda lengua suficientemente consolidada para interiorizar conceptos matemáticos. De todas maneras, las variables serían múltiples, empezando por el contexto en el que se aplique, ya que puede considerarse bilingüe pero puede tener o no una política clara de la enseñanza de contenidos, lo cual implicaría tener programas consolidados, profesores entrenados en metodologías específicas y material adecuado, atendiendo a algunas características que pertenecen al AICLE; o analizando el contexto matemático, que de grado a grado maneja contenidos más complejos.
Atendiendo a este último aspecto, como una implicación a largo plazo, esta estrategia podría ser de beneficio para la institución, ya que este contexto en particular maneja el área de matemáticas en español en los grados superiores, lo que podría contribuir al reconocimiento del vocabulario especializado. Igualmente, gracias a la realización de la investigación, y como aprendizaje personal, es ahora evidente la manera en que la institución avanza hacia la construcción de la política de lengua.
Una limitación de la investigación podría verse reflejada en el efecto que podría tener la aplicación de la estrategia preview-view-review durante el proceso de adquisición de la segunda lengua, ya que se podría pensar que al usar la lengua materna, de alguna manera afectaría el proceso, pero se puede intuir, de la investigación y del seguimiento previo y posterior de los grupos que participaron del estudio, que la estrategia no actúa como un ente negativo sino que, por el contrario, permite hacer conexiones entre una lengua y la otra para beneficio del contenido académico. Más específicamente, al comparar el desempeño de las estudiantes de los dos grupos antes y después de la intervención con respecto a la segunda lengua como tal, no se evidenció ningún cambio que permitiera concluir que la estrategia contribuye al mejoramiento de la segunda lengua, pero claramente sí está demostrado que favoreció el desempeño académico del contenido matemático en inglés de las estudiantes del grupo experimental. Por lo tanto, se sugiere que al usar la estrategia en un ambiente bilingüe para enseñar matemáticas valdría la pena hacer un seguimiento cuantitativo y cualitativo del desempeño de los estudiantes, tanto en matemáticas como en inglés.
Otra de las limitaciones del estudio podría representarse en las diferencias que pueden existir entre las docentes e incluso entre un grupo y otro, ya que se podría pensar que la estrategia preview-view-review no fue determinante para obtener un mejor desempeño sino el nivel de matemáticas de cada docente o su estilo de enseñanza o incluso la experticia que tenga enseñando el contenido o manejando grupos de ciertas edades. Para lo que tiene que ver con el presente estudio, si bien las docentes han tenido experiencias diferentes en el área, cada una de las actividades y evaluaciones se planeó en conjunto con la jefe de Departamento de Matemáticas, y las clases fueron concebidas y ejecutadas de tal manera que ninguna de las docentes hiciera algo diferente a lo acordado anteriormente (vale la pena aclarar que es así como generalmente se trabaja en la institución en donde se realizó el estudio).
Finalmente, estas reflexiones podrían tomar el rol de sugerencias para la institución analizada, ya que muchos de los aspectos mencionados podrían ser parte de alguna metodología mencionada anteriormente como CLIL o CBI, atendiendo precisamente a lo que García (2009) plantea con respecto a la importancia de tener acuerdos de lengua, los cuales podrían brindar una guía al educador y a la institución educativa.