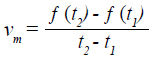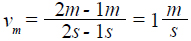INTRODUCCIÓN
La SE es un enfoque de investigación en Matemática Educativa que nació en México en la década de los noventa; se fundamenta en la idea que el conocimiento se construye socialmente (Cantoral, 2013), en donde el individuo interactúa con su entorno, lo cual desencadena una anidación de prácticas (acción, actividad, prácticas, prácticas de referencia y prácticas sociales), que se discuten más adelante; la SE también critica el discurso Matemático Escolar del cálculo (Camacho, 2006), debido a que argumenta que éste no tiene en cuenta la relación que el conocimiento matemático guarda con la anidación predicha, que lo acompaña y es vital e importante en su origen y construcción. Lo anterior es significativo para el entendimiento del aprendizaje desde la SE, en especial del aprendizaje de las matemáticas, puesto que esta teoría defiende la idea que el conocimiento se construye social y contextualmente a partir prácticas sociales normadas. Uno de sus objetivos fundamentales es “caracterizar los usos y las resignificaciones del conocimiento matemático situacionalmente, puestos en la dialéctica del conocimiento matemático y de la vida, es decir; ponerse en el uso del conocimiento matemático de la gente” (Cordero et al., 2014, p. 88).
A continuación se enuncia una caracterización de la SE, la cual nos ayuda a comprender el estado actual de este enfoque.
La Teoría Socioepistemológica de la Matemática Educativa se ocupa del estudio de fenómenos didácticos ligados al saber matemático asumiendo la legitimidad de toda forma de saber, sea este popular, técnico o culto, pues considera que ellas, en su conjunto, constituyen la sabiduría humana. Así el programa socioepistemológico se caracteriza por explicar la construcción social del conocimiento matemático y la difusión institucional. Ello precisa de rupturas con los programas clásicos en Matemática Educativa. (Cantoral, Reyes y Montiel, 2014, p. 1)
En este artículo se describe y analiza el proceso de construcción de conocimiento sobre el concepto de derivada de una función en un punto (velocidad instantánea) que un grupo de estudiantes lleva a cabo. Esto se hace desde la identificación y el detalle de prácticas socialmente compartidas desarrolladas por dichos estudiantes, dentro de las cuales se encontraron las prácticas de medición, manejo de datos, visualización, graficación, aproximación y predicción.
El interrogante del presente artículo parte de otro más general, relacionado con una investigación desarrollada en la Universidad Pedagógica y Tecnológica de Colombia (UPTC) que intentó describir cómo un grupo de estudiantes construyó el concepto de derivada en un punto, a partir de una secuencia didáctica centrada en el contexto y la actividad humanos. La primera actividad de la secuencia se detalla en Espinosa y Jiménez (2014); allí se pueden encontrar similitudes con el presente escrito referentes al paradigma epistemológico, metodológico, pedagógico y didáctico, ya que el citado parte de la investigación mencionada. La originalidad del presente escrito está en mostrar la fase final de la investigación realizada, es decir, en dar cuenta de la totalidad de la investigación, ya que es en esta fase en donde se logra el objetivo general. También cabe mencionar que aquí se realiza una construcción de conocimiento que requiere conceptos más complejos que los necesarios en la primera actividad señalada, los cuales fueron construidos por los estudiantes en la secuencia didáctica citada, es decir, una de las bases de la actividad tratada aquí es la construcción de conocimiento realizada en Espinosa y Jiménez (2014). En dicho artículo no se tienen en cuenta las prácticas de aproximación y predicción, las cuales son de vital importancia en lo que sigue. Es importante mencionar que el concepto tratado en el artículo citado es de carácter estático, mientras que en el presente es dinámico.
La importancia del artículo radica en presentar una posibilidad distinta a la tradicional de ver el aprendizaje del concepto de derivada en un punto; dicha posibilidad concibe que el estudiante construye conocimiento matemático a partir de sus acciones, actividad, prácticas, prácticas de referencia y prácticas sociales situadas en un contexto. Con base en lo dicho se afirma que el conocimiento no se transmite del profesor al estudiante de forma espontánea; concibiéndose aquí una forma alternativa para abordar las temáticas mencionadas. En consecuencia, se asume que el alumno, más que memorizar, construye conocimiento, lo cual garantiza un aprendizaje significativo.
La SE critica la enseñanza tradicional argumentando que ésta no considera las prácticas sociales como factores que influyen en la construcción de conocimiento y que tiene una visión pobre sobre el aprendizaje de las matemáticas, ya que fundamenta la enseñanza en el desarrollo de la habilidad algorítmica del estudiante, es decir, la solución mecánica de ejercicios. En la enseñanza tradicional el conocimiento se da al estudiante, no se permite una construcción, se interpreta como acabado. Por tanto los socioepistemólogos proponen una reorganización del currículo matemático escolar fundamentándolo en las prácticas sociales, de donde es imperativo construir marcos de referencia a partir de investigaciones socioepistemológicas.
El presente escrito se organiza de la siguiente forma: en la sección inicial se expone de manera general lo que se entiende por práctica social en el enfoque socioepistemológico. En segunda instancia se presenta someramente la teoría socioepistemológica, mencionando algunas de sus premisas, objeto de estudio, principal problema identificado en la enseñanza del cálculo y posible solución propuesta a este problema. En la tercera parte se exhibe la metodología clásica empleada en proyectos de investigación basados en la SE. Finalmente, se analiza cómo un grupo de estudiantes construyó el concepto derivada en un punto, a partir de una secuencia didáctica centrada en el contexto y la actividad humanos.
PRÁCTICA SOCIAL EN EL ENFOQUE SOCIOEPISTEMOLÓGICO
El conocimiento matemático surge a partir de la actividad humana, es decir, se aprende haciendo; el hacer es fuente para que el saber emerja y se constituya como tal. Como el obrar humano está normado por prácticas consensuadas que regulan las relaciones humanas, invariantemente la práctica humana se entiende como práctica social normada, es decir, el conocimiento tiene su origen en prácticas sociales normadas (Cantoral, 2004).
Para Arrieta et al. (2004), el análisis investigativo socioepistemológico se debe centrar en la relación entre las prácticas sociales y el conocimiento, “entendiendo a las prácticas sociales como un conjunto de acciones voluntarias que, intencionalmente desarrolla el individuo para construir conocimiento” (p. 418). Es de resaltar que la anterior es una definición inicial de práctica social, y actualmente este concepto se entiende de una manera distinta en la SE.
Para el presente artículo nos basamos en la siguiente definición de práctica social, enunciada por Pérez y Morales (2013): “Existen actividades que nacen al interior de las comunidades y que pueden generar conocimientos que luego son inmersos en el sistema escolar. Una vez ahí, muchas veces no se tiene en cuenta su origen epistemológico y además no se cuenta con una coordinación entre estos conocimientos y la forma como se vinculan e influyen directamente –o indirectamente– en la vida del estudiante. En la teoría socioepistemológica estas actividades pueden ser reconocidas como prácticas sociales” (p. 7694).
Para la SE, aludiendo a Cantoral, Reyes y Montiel (2015), las prácticas sociales no se filman, se infieren, es decir, estas no son observables, son el resultado de un análisis y de una problematización del saber. Son, en ese sentido, emergentes sociales que se localizan en un particular juego de prácticas, “la anidación de prácticas” (acción-actividad-práctica- práctica de referencia-práctica social).
Es común a lo largo del texto llamar a las prácticas que aparecen en tercer lugar de la anidación predicha prácticas socialmente compartidas; por tanto, cuando se hable de prácticas se entenderá que se habla de estas segundas. Para el presente escrito, el análisis del último apartado se centra en prácticas socialmente compartidas, las cuales se relacionan en el artículo con la práctica social del praediciere y las prácticas de referencia temporalización, secuenciación, algebrización y predicción. Este énfasis en el análisis se sustenta en que en sus investigaciones, para Cantoral et al. (2006), “los socioepistemólogos reportan más bien caracterizaciones del ejercicio de las prácticas que anteceden a la producción o construcción de conceptos y al desarrollo del saber” (p. 85). El praediciere se define como “acción intelectual del sujeto epistémico sobre los datos fácticos para establecer patrones de regularidad del comportamiento de lo que ha de predecirse. Acción que tiene efecto, sólo con el conocimiento de las explicaciones causales de los fenómenos estudiados” (Minguer, 2006, p. 21).
El término acción establece que una persona, animal o cosa (material o inmaterial) está haciendo algo, está actuando (de manera voluntaria o involuntaria, de pensamiento, palabra u obra), lo que normalmente implica movimiento o cambio de estado o situación y afecta o influye en una persona, animal o cosa. Comúnmente se entiende por actividad un conjunto de acciones que lleva a cabo un individuo o una institución cotidianamente, como parte de sus obligaciones, tareas o funciones.
Consideramos importante en este punto traer a colación lo siguiente, lo cual nos da un panorama de cómo se entiende desde la SE el operar de las matemáticas en las diferentes culturas, por medio de la anidación acción-actividad-prácticas, prácticas de referencia y prácticas sociales.
[…] las Matemáticas no se inventaron para ser enseñadas y sin embargo se enseñan, se las usa en distintos escenarios, digamos que “viven” a través de las acciones más básicas de toda actividad humana: construcción de vivienda, actividades de siembra y tejido, elaboración de protocolos para el empleo de fármacos o de tóxicos, elaboración de recetas de cocina, diseño de depósitos de vino, cálculo de dosis médicas, explicitación de conjeturas matemáticas, coordinación de movimientos de un piloto al aterrizar en una pista complicada, matematización de fenómenos biológicos, toma de decisiones para inversiones financieras, interpretaciones de la opinión pública, simulación de flujos continuos, trueque en mercados tradicionales, estudio de la consolidación de suelos finos saturados, de mecanismos regulatorios de temperatura en la industria química… Están presentes también en la educación formal, en las aulas de ciencias, Física, Química, Biología, tecnología, taller, lectura y comprensión… y, por supuesto, en la clase de Matemáticas. Están presentes en las prácticas cotidianas de todos los seres humanos cuando clasifican, predicen, narran, comparan, transforman, estiman, ajustan, distribuyen, representan, construyen, interpretan, justifican, localizan, diseñan, juegan, explican, cuentan o miden. (Cantoral, Montiel y Reyes, 2015, p. 15)
En lo que sigue de este apartado nos referiremos a las prácticas, según una clasificación debida a Camacho (2006).
Según Camacho (2006), las prácticas centradas en el conocimiento se dividen en dos grupos: “las vinculadas a los cambios del conocimiento por actividades extradidácticas, y otras, en las que el uso del conocimiento se ejerce en el salón de clase mediante actividades Didácticas” (p. 135).
Para la socioepistemología son importantes ciertas prácticas para la construcción de conocimiento, las cuales se denominan procedimentales. Camacho (2006) divide estas prácticas en dos grandes grupos: “aquellas donde el conocimiento matemático, en todas sus formas, toma definición en actividades de la ingeniería como la observación; y las actividades de corte experimental, como la simulación y modelación, donde se colocan el pensamiento y el lenguaje variacional” (p. 149). Las prácticas procedimentales de simulación y modelación consisten en traducir una situación a un lenguaje de alguna disciplina, en nuestro caso las matemáticas, con base en algunos elementos extraídos de ella (variables, constantes, símbolos, conceptos, etc.). La tarea fundamental es establecer una interacción entre la lógica de tales elementos y la situación real, lo cual permite a los estudiantes desarrollar ciertas habilidades importantes en el pensamiento matemático. Camacho (2006) menciona que tales habilidades pueden ser esquematizar, formular y visualizar un problema de diferentes maneras, predecir situaciones, descubrir relaciones y regularidades, entre otras.
La socioepistemología se enfoca en el segundo grupo de prácticas, puesto que uno de sus objetivos iniciales es intervenir en el diseño de situaciones para establecer marcos de referencia centrados en prácticas sociales que permitan el desarrollo del pensamiento y del lenguaje variacional, y de cambio. Por ejemplo, en el trabajo de Buendía y Cordero (2002, citados en Camacho, 2006), el trabajo epistemológico llevó a concluir que “Euler estuvo involucrado en actividades por las cuales tuvo necesidad de formalizar las funciones periódicas” (p. 146). La práctica que favoreció esta formalización “[…] fue la descripción de un movimiento que ocurre en el tiempo”, al manejar éste como la variable independiente. Esta descripción llevó a Buendía y Cordero a crear una situación didáctica con la que se buscó que los involucrados establecieran patrones de regularidad con lo periódico y desarrollaran la práctica de predicción mediante recursos gráficos.
Dentro de las prácticas de simulación encontramos las actividades de graficación y manejo de datos, que en la socioepistemología se consideran como generadoras de conocimiento en sí mismas y no sólo como actividades de apoyo didáctico. Según Camacho (2006), las propuestas didácticas que parten de las prácticas de simulación tienen tres características fundamentales: la selección de las prácticas sociales a través del lenguaje de los objetos matemáticos en juego, el carácter discursivo de la construcción social del conocimiento y las interacciones en el aula.
Para Abric (2001), el análisis de toda práctica social supone que se tengan en cuenta al menos dos factores esenciales: “
Las condiciones sociales históricas y materiales en las que ella se inscribe, por una parte, y por la otra, el modo en el que se apropia el individuo, o grupo concerniente, proceso en el cual los factores cognitivos, simbólicos y representacionales desempeñan un papel determinante” (citado en Camacho, 2006, p. 134).
De aquí que la práctica sea inseparable del contexto, ya que a partir del mismo surgen ciertos conceptos y teorías matemáticos, provocados por las prácticas que en éste generan, tesis defendida por la socioepistemología.
LA SE Y EL DISCURSO MATEMÁTICO ESCOLAR
El fenómeno de aprendizaje de las matemáticas es trivial cuando se asume (como hace un tiempo) que el aprendizaje se lleva a cabo por medio de la transmisión de conocimientos. En este sentido, sería natural que se considerara suficiente para el aprendizaje de las matemáticas que un sujeto (profesor) tuviese conocimientos en matemáticas para poder transmitir a otros (estudiantes) tales conocimientos. En esta perspectiva, los libros clásicos de cálculo serían óptimos para el aprendizaje de las matemáticas.
Actualmente el fenómeno de aprendizaje se acepta como más complejo y se considera que el profesor debe tener, junto con el conocimiento matemático, también otro, denominado didáctico, el cual depende de la concepción epistemológica que se tenga de las matemáticas (Jiménez et al., 2010). Además se asume que el conocimiento no se transmite, sino que más bien se construye socialmente en un contexto. Lo anterior es compartido por la SE, en donde adicionalmente se parte del hecho de que el conocimiento matemático se construye a partir de prácticas sociales (Cantoral, 2004). La SE es una perspectiva múltiple que concibe el fenómeno de aprendizaje de las matemáticas en cuanto interacción de las dimensiones: epistemológica del conocimiento matemático, sociocultural (y por ende contextual), cognitiva y didáctica (Ferrari, 2004).
El objeto de la SE es la construcción social de conocimiento matemático. Los socioepistemólogos argumentan que el conocimiento matemático va acompañado en su construcción de prácticas sociales y un entorno. Los objetos matemáticos emergen de dichas prácticas, las cuales no sustituyen a los objetos matemáticos, más bien acompañan a estos en su proceso de construcción y constitución por parte del humano (Cantoral, 2011).
Los socioepistemólogos aducen que el discurso Matemático Escolar clásico no tiene en cuenta la naturaleza propia del saber, ni considera que el conocimiento sea situado y vaya acompañado de la actividad humana. El discurso referido es de carácter expositivo, con lo cual se interpreta que éste concibe al conocimiento como una transmisión y no como una construcción social contextual. En los textos criticados también encontramos que, al menos en el cálculo, prevalece lo algorítmico sobre, por ejemplo, lo visual y contextual, lo cual hace que los estudiantes aprendan como robots reglas de derivación, reglas de integración, etc., sin tener conciencia de los conceptos que envuelven dicha algoritmia.
En contraste con cómo se plantea en la exposición tradicional de los libros de cálculo, la SE propone un aprendizaje contextual, en donde éste se presente como una herramienta para entender fenómenos del entorno en el que se desenvuelve quien aprende: “el papel que desempeña el cálculo en el currículo debe ser el de medio o herramienta que le permita al estudiante entender la realidad de otras áreas del conocimiento; [en tal dirección] deberíamos estudiar las dificultades del aprendizaje” (Salinas y Alanís, 2009, p. 366).
La crítica del discurso Matemático Escolar clásico es el punto de partida para definir el principal problema de la enseñanza del cálculo, según los socioepistemólogos; para sustentarlo encontramos a Cantoral, Cordero, Farfán e Imaz (citados en Salinas y Alanís, 2009, p. 360), quienes señalan que la estructura formal de la obra matemática es la menos propicia para comunicar las ideas del cálculo. Los autores establecen que el aprendizaje del cálculo es para futuros usuarios de este, pero aclaran que no están a favor de técnicas como el empleo de rutinas algorítmicas.
La presentación formal de las definiciones del cálculo en los libros de texto termina con aplicaciones de estas, que dejan la impresión de ser consecuencia inmediata de la teoría. El índice de libros de texto tradicionales muestra ese tipo de estructura en el contenido: números reales, funciones, límites, continuidad, derivada, aplicaciones de la derivada, integral y aplicaciones de la integral (Salinas y Alanís, 2009). Lo precedente es contradictorio con la historia, en donde, por ejemplo, se evidencia que la construcción del concepto de derivada parte de problemas concretos y contextuales, junto con prácticas como la predicción y aproximación, entre otras; el desarrollo del concepto y su algoritmia ocurren después de la exploración de dichos problemas. La construcción de conocimiento se ve afectada por esta visión del aprendizaje como la simple memorización: “Una de las características del discurso Matemático Escolar tradicional ha sido centrarse en las definiciones, tal vez, por ello, deja de lado ciertos marcos de referencia donde pudiera resignificarse la matemática” (Ordóñez y Buendía, 2007, p. 427). La SE es consciente de tal problema, y por su parte considera como hipótesis que la actividad es la fuente de reorganización de la obra matemática y del rediseño del discurso Matemático Escolar.
La SE tiene entonces como objetivo fundamental contribuir a la construcción de los mencionados marcos de referencia, basados en propuestas centradas en las prácticas sociales que buscan resignificar el conocimiento matemático escolar, y por tal razón pretende llegar a “construir epistemologías de prácticas que, por un lado, amplíen la explicación de los fenómenos de construcción de conocimiento y, por otro, fundamenten el rediseño del discurso Matemático Escolar” (Montiel y Buendía, 2011, p. 446).
METODOLOGÍA
Sobre la metodología socioepistemológica (Cantoral, 2011)
La SE es una teoría que tiene una base empírica, es decir, se ha construido con el estudio previo de la realidad, tratando de entenderla; no es una teoría preexistente que se aplica a la realidad, más bien emerge de ella.
La SE no se reduce a definir términos; la filología es la que se ocupa de ello. La primera busca intervenir en la realidad, la segunda no. Por lo expuesto, en la SE se aceptan caracterizaciones diversas de una misma noción. El método de investigación en SE no se reduce a una definición tradicional positivista de método, puesto que ésta no se ocupa de encontrar verdades y definirlas.
Por las características de la teoría socioepistemológica, hablar de un método puede ser contradictorio, y en efecto lo es. Se habla de un esquema, más que de un método, el cual no se usa para hallar verdades (como se presume en la ciencia positivista), sino para caracterizar fenómenos. El fin de la SE es la construcción social de conocimiento de forma; con base en ello, las investigaciones de corte socioepistemológico comparten tres características esenciales en cuanto esquema metodológico:
• Se debe hablar sobre la naturaleza del saber. Se trata sobre una naturaleza misma del saber. Hablar del saber no se limita, en esta perspectiva, a definir la relación que éste guarda con los objetos matemáticos, sino que posiciona al ser humano en sus distintas dimensiones, en el acto mismo de construcción de sus sistemas conceptuales. Se trata de responder a las preguntas ¿cómo las personas actúan en la construcción de sus conocimientos? y ¿cómo aprenden las personas de acuerdo a su relación con el saber en contexto?
• La práctica social es normativa de la actividad humana y es base para construir conocimiento. Se responde a la pregunta ¿qué nos hace hacer lo que hacemos? Para el presente artículo se traduce como ¿qué prácticas nos permiten construir el concepto de derivada en un punto desde un contexto particular?
• Se realizan articulaciones teóricas con base en una fuerte evidencia empírica. Se ocupa de caracterizar las articulaciones teóricas con una fuente de evidencia empírica. Lo anterior se puede evidenciar a lo largo del análisis en la última sección, en donde se toma información de diversas fuentes que constituyen la evidencia empírica, tales como Diario de Campo, videos y documentos, en donde los estudiantes realizaron las actividades.
La secuencia didáctica elaborada, de la cual hace parte la actividad analizada en el presente artículo, tiene como base el esquema metodológico socioepistemológico, cuyo esbozo se puede consultar en Espinosa y Jiménez (2014).
Análisis de contenido
Para Romero (2013), “el análisis de contenido es un método para el procesamiento y revisión de las dimensiones cuantitativas (médium) y cualitativas (mediador) de los contenidos de la comunicación” (p. 16). La utilidad de este método está en que permite “[…] formular, a partir de ciertos datos, inferencias plausibles y válidas que puedan aplicarse a su contexto” (Krippendorff, 1990, citado en Romero, 2013, p. 16).
Método del análisis de contenido
El análisis de contenido se ocupa de la naturaleza del mensaje en un discurso. Su finalidad es ahondar sobre la estructura interna de la comunicación, estudiando para ello su estructura semántica.
Para Cohen, Manion y Morrison,
El término análisis de contenido indica el proceso de recogida y resumen de datos escritos–los contenidos principales de dichos datos y sus mensajes. De modo más preciso, define un conjunto de procedimientos estricto y sistemático para el análisis riguroso, el examen y verificación de los contenidos de datos escritos. Algunos autores lo definen como una técnica de investigación para elaborar inferencias válidas y replicables a partir de textos (u otros materiales escritos) en aquellos contextos en que se utilizan. Por texto se entiende cualquier material de comunicación escrita, que se suponen deben ser leídos, interpretados y entendidos por otras personas distintas de aquella que los analiza. El análisis de contenido se puede llevar a cabo con cualquier tipo de material escrito, desde documentos impresos a transcripciones de entrevistas, desde productos de los media hasta producciones escritas. Se utiliza frecuentemente para analizar un número considerable de textos, debido a su naturaleza sistemática, gobernada por reglas; también permite utilizar el análisis asistido por ordenador. Utiliza la categorización para reducir grandes cantidades de datos. (2011, citados en Romero, 2013 p. 17)
Esta técnica se empleó en el presente artículo en cuanto al análisis de los textos entregados por los estudiantes, correspondientes a la solución de la actividad.
La metodología mencionada permite descomponer un discurso en sus unidades más simples, para lo cual utiliza de modo sistemático la determinación de temas y la identificación de categorías. La aplicación de esta técnica en la investigación educativa puede ayudarnos a:
• Descubrir recurrencias en el discurso.
• Contrastar hipótesis.
• Deducir significados en un texto (Romero, 2013).
Metodología de clase
En la investigación de la cual se desprende el presente artículo se elaboró una secuencia didáctica que se direcciona a la construcción del concepto de derivada en un punto, y se optó por el siguiente orden en la construcción de los conceptos: razón matemática (razón constante y variable), razón promedio y razón promedio de cambio, límite de una función en un punto, continuidad de una función en un punto y razón instantánea de cambio; la descripción y el análisis de la construcción de conocimiento evidenciada aquí hacen parte de la actividad final de tal investigación. La secuencia se elaboró con base en situaciones contextuales en las que los estudiantes estuvieron implicados. El contexto de las situaciones estuvo determinado por la carrera profesional en la que los alumnos están inscritos: Física, de la Facultad de Ciencias Básicas de la UPTC, en donde se trabajó con el concepto de velocidad. El propósito fue construir, con el concepto de razón media y razón promedio de cambio, el de velocidad media, y luego el de la velocidad instantánea, que se constituye en el de derivada en un punto.
El desarrollo de las actividades se realizó en tres etapas: una de trabajo individual, otra de trabajo grupal y una plenaria; en esta última se socializa, se confrontan interpretaciones y soluciones y se buscan consensos (Jiménez, Suárez y Galindo, 2010).
La construcción social del conocimiento es una tesis fundamental en la SE (Camacho, 2006). En todas las actividades de clase se refleja una selección de prácticas de las que se parte para la construcción social de conocimiento, y se destacan las interacciones importantes en el aula de clase. La actividad correspondiente al presente artículo se grabó en video; por tal razón, se hace alusión a los videos 1, 2 y 3 a lo largo del análisis de la construcción de conocimiento.
CONSTRUCCIÓN SOCIAL DEL CONCEPTO DE DERIVADA DE UNA FUNCIÓN EN UN PUNTO
Consideraciones iniciales
Actividad individual (ver el anexo 1)
Aquí se realizó un recuerdo del concepto de velocidad media entre dos tiempos con base en una función de posición de R en R, el cual fue construido en una actividad anterior. Fue necesario hacer esto porque se requirió para el desarrollo de la actividad que se analiza ahora. En primera instancia se presenta el concepto como modelo (aspecto algebraico), proporcionándose la fórmula de velocidad media entre dos puntos, dada una función. En segundo lugar se enfatiza la representación geométrica (pendiente de recta secante entre dos puntos de una función); en la actividad esto se muestra en la figura 1 (ver el anexo 1), en donde se encuentra la gráfica de la función f (x).
Actividad grupal y plenaria (ver el anexo 1)
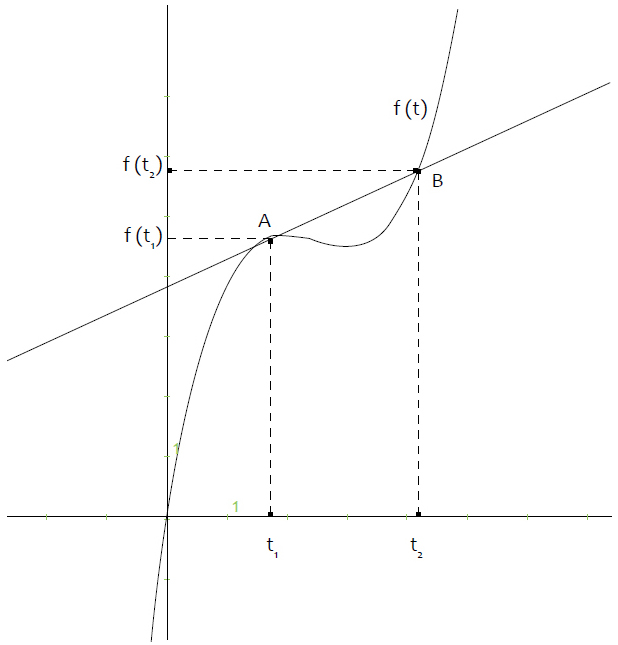
Los estudiantes se organizaron en seis grupos de trabajo. En la actividad final se tomó un punto fijo de la función f (t) que aparece en la figura 2 (ver el anexo 1), el cual es el punto (1,1), junto con otros dos puntos: (2,2) y (1.5, 1.32) en la misma gráfica, y se presentó el cálculo (práctica de medición) de la velocidad media entre el punto fijo y los otros dos citados.
El propósito de la actividad fue construir el concepto de derivada de una función en un punto a través del paso al límite de la velocidad media para llegar al tanteo de la velocidad instantánea en el punto (1,1), junto con el apoyo de las prácticas de visualización, medición, aproximación y predicción (el concepto límite fue construido en una actividad anterior). Dicha construcción dentro de diferentes lenguajes: numérico, algebraico y visual. Con esta actividad se concluyó la investigación, puesto que con ella se dio cumplimiento total al objetivo general de esta.
La figura 2, en la que sólo aparecen como valores numéricos las escalas fijadas para el eje y y x (ver el anexo 1), fue base para que el estudiante encontrara puntos cercanos al punto (1,1) (noción de límite) por medio de la visualización y, posteriormente, hallase una aproximación a la velocidad instantánea en dicho punto por medio de la medición de velocidades medias entre el punto (1,1) y los cercanos escogidos al mencionado, lo cual permitió realizar una predicción o conjetura del valor de la velocidad instantánea en (1,1).
Los puntos 1 al 6 permitieron realizar lo mencionado anteriormente en el propósito de la actividad. El punto 5 y el 6 (plenaria; ver el anexo 1) fueron de vital importancia para la interpretación geométrica del concepto de velocidad instantánea, como se verá a continuación.
Análisis de la actividad
No se analiza la actividad individual, ya que esta consistió en la lectura de información correspondiente al conocimiento que el estudiante había construido previamente en actividades anteriores.
Actividad grupal y plenaria
La presente actividad se desprende de una secuencia didáctica elaborada con base en un estudio del movimiento; por tal motivo, la problematización del saber consistió en cómo describir el movimiento de un objeto, en particular sus velocidades media e instantánea. La secuencia citada se elaboró teniendo en cuenta la práctica social mencionada con anterioridad y las prácticas de referencia predichas. A continuación se hace énfasis en el análisis de cómo ciertas prácticas intervinieron como acompañantes de la construcción de conocimiento del tema que estamos tratando. Como es usual en un estudio de carácter socioepistemológico, las actividades de la secuencia didáctica se elaboraron teniendo en cuenta las prácticas de referencia que se identificaron como adecuadas, luego de hacer un examen epistemológico del concepto que se pretende construir en el aula de clase; el objeto de este artículo no es profundizar en este estudio. Para el presente concepto se identificaron las prácticas de referencia temporalización, secuenciación, algebrización y predicción. La secuenciación trivialmente se ve plasmada en el diseño de la secuencia citada. El estudio del movimiento envuelve con fuerza el componente de la temporalización. Al respecto, podemos mencionar a Buendía y Cordero (2002, citados en Camacho, 2006), cuyo trabajo epistemológico llevó a concluir que “Euler estuvo involucrado en actividades por las cuales tuvo necesidad de formalizar las funciones periódicas” (p. 146). La práctica que favoreció esta formalización “[…] fue la descripción de un movimiento que ocurre en el tiempo”, al manejar éste como la variable independiente.
Se interrogó a los estudiantes sobre el significado de las dos velocidades medias presentadas en la actividad grupal (ver el anexo 1) como aproximaciones a la velocidad instantánea en el punto (1,1). En el video 1 (04:15) se aprecia cómo el grupo 2 afirmó que las velocidades medias dadas en la actividad no son aproximaciones a la velocidad instantánea en (1,1), con el argumento que los puntos tomados en la actividad para calcular dichas velocidades medias “no son muy cercanos al punto (1,1)”, aquí observamos las prácticas de narración, comparación, interpretación, justificación y explicación. Hay confusión en el término aproximación, puesto que el grupo no consideró que los acercamientos a la velocidad instantánea a través de las velocidades medias citadas podrían ser “distantes de la velocidad instantánea”, tal como insistió el profesor, el cual clarificó el concepto e invitó a los estudiantes a ver que ciertas estimaciones de un resultado pueden ser cercanas o lejanas a éste, tal como se aprecia seguidamente en la grabación, lo cual sugiere existencia de buenas o malas estimaciones y, por tanto, de buenas o malas aproximaciones; en este acto vemos las prácticas de justificación y explicación, así como la práctica de simulación manejo de datos.
El grupo 4 (video 1, 08:10), al igual que el grupo anterior, presentó dificultad en entender el sentido de la velocidad media entre dos puntos como un tanteo de la velocidad instantánea en cualquiera de ellos. En contraste, el grupo 5 (video 1, 10:24) no tuvo la dificultad referida anteriormente. Afirma que las velocidades medias calculadas con el punto (1,1) y otros de la gráfica de f (x) son mejores tanteos de la instantánea en (1,1), conforme se tomen puntos cada vez más cercanos al (1,1) en dicho cálculo, con lo cual podemos ver cómo las prácticas de medición y estimación acompañan esta etapa de la construcción de conocimiento.
A continuación veremos cómo evolucionaron las concepciones de los estudiantes en la actividad, con base en el análisis de la documentación entregada por ellos.
Cinco grupos contestaron que las velocidades citadas son presunciones de la velocidad instantánea en el punto (1,1), apoyando su respuesta en las nociones de cercanía y lejanía; en este punto vemos cómo se enlazan las prácticas de narración, justificación, estimación, aproximación entre sí, y cómo las anteriores se armonizan con la práctica de referencia predicción y la práctica social del praediciere, en el sentido de “preparar el terreno de la clase” para identificar los patrones de regularidad del comportamiento de lo que ha de predecirse (Minguer, 2006). En los siguientes grupos, 2, 4 y 5, respectivamente, vemos las ideas de acercamiento y alejamiento del valor real de la velocidad instantánea en (1,1) con base en el cálculo de velocidades medias entre el punto (1,1) y puntos cercanos o lejanos a éste en la gráfica. Claramente se observan las ideas de cercanía y lejanía de puntos en la gráfica respecto al punto fijo (1,1) (idea que se lleva a cabo mediante la visualización de la figura 2); esta idea fue base para comprender la noción de límite de una función en un punto (desarrollada en una actividad anterior) y para posteriormente construir el concepto de velocidad instantánea en un punto (derivada en un punto). En los dos primeros grupos mencionados se aprecia explícitamente que para hallar una aproximación a la velocidad instantánea en (1,1) a través de velocidades medias se precisa de la presencia de este punto en el cálculo de la velocidad instantánea. Esto último nos dice que los estudiantes se percataron de que se “debe tener cuidado” en la práctica manejo de datos y medición de las velocidades medias para realizar estimaciones adecuadas y, por tanto, una conjetura o predicción. En el primer y último fragmento nos damos cuenta de cómo los estudiantes han identificado la existencia de mejores y peores aproximaciones.
El grupo restante (grupo 6) emitió un juicio incoherente respecto a la respuesta de la presente pregunta, aunque hay una idea respecto a la toma de puntos próximos al punto (1,1) en la figura 2. Aquí, la práctica de interpretación se llevó a cabo de forma incorrecta, pero los estudiantes superaron dicha dificultad conceptual con el apoyo del docente y compañeros a lo largo de la clase, lo cual se logró gracias a la elaboración de la secuencia didáctica y a la puesta en práctica de esta a partir de la SE, la cual tiene bases de constructivismo social.
En la pregunta 2 se interrogó a los estudiantes sobre cuál velocidad media de las dos mostradas en la actividad grupal es mejor aproximación a la instantánea en (1,1). Todos los grupos contestaron que la velocidad media medida entre el punto (1,1) y (1.5, 1.32) es más próxima a la velocidad instantánea en (1,1) que la medida entre el punto (1,1) y el punto (2,2). Todos los grupos fundamentaron su respuesta en la idea de cercanía, por cuanto el punto (1.5, 1.32) de la gráfica de f(t) es más cercano al punto (1,1) que el punto (2,2). Los estudiantes concluyeron que los resultados de calcular velocidades medias entre puntos de una gráfica de posición contra tiempo, cuando uno de ellos es fijo, son mejores aproximaciones numéricas a la velocidad instantánea en el fijo, conforme se tomen en la gráfica puntos cada vez más cercanos a este último para dicho cálculo; de esta forma, se pasa de un lenguaje geométrico a uno numérico, y viceversa. Lo enunciado nos permite inferir el uso de dos prácticas más por parte de los estudiantes, la localización, comparación y la clasificación, en pro de realizar una predicción (práctica de referencia). Como ya se mencionó, en la SE la práctica de visualización se concibe como propiciadora de construcción de conocimiento matemático; esto se deduce de lo descrito, en cuanto a la clase, en la segunda pregunta de la actividad.
En el video 1 (11:50) se visualiza cómo el grupo 1 argumentó que las velocidades medias medidas entre (1,1) y otros puntos de la gráfica son mejores conjeturas de la velocidad instantánea en (1,1), conforme se tomen puntos cada vez más cercanos a (1,1). En el mismo video 1 (13:40) se muestra cómo el grupo 5 llegó a una conclusión importante en la actividad “la velocidad media es siempre una aproximación a la velocidad instantánea”; con lo que se concluye que los estudiantes en este punto desarrollaron habilidades en cuanto a descubrir relaciones y regularidades, y es una fase previa para llevar a cabo una modelación de la velocidad instantánea en un punto con el uso de la velocidad media, es decir, “se prepara el terreno” para llevar a cabo la práctica de modelación.
En el mencionado video (14:25) se ve que el profesor pidió a todos los estudiantes que observaran que en el cálculo realizado para las velocidades medias presentadas en la actividad siempre se tomaron las coordenadas del punto (1,1); lo anterior es de gran utilidad en todas las preguntas de la actividad. También se especificó que en la gráfica de f(t) en la figura 2 se debían elegir puntos cuyas coordenadas se tendrían que fijar por medio de la visualización y la escala de los ejes.
Más adelante (16:40) se observa que en el grupo 4 persistió la confusión en cuanto a la noción de aproximación; el profesor se vio en la necesidad de dar un ejemplo con edades a dicho grupo. A continuación exhibimos las respuestas de dos grupos (4 y 5, respectivamente) respecto a la pregunta 2.
El propósito de la pregunta 3 (ver el anexo 1) fue que los estudiantes hallaran aproximaciones a la velocidad instantánea en (1,1), diferentes a las mostradas en la actividad grupal, a través del tanteo del valor de las componentes de puntos de la gráfica de f(t) en la figura 2 (práctica de visualización), para que posteriormente se calcularan por medio de la práctica de medición de las velocidades medias entre (1,1) y los puntos estimados en la gráfica. Se buscó también que los estudiantes llegaran a una apreciación del valor real de la velocidad instantánea en el punto (1,1) por medio de las prácticas de aproximación y predicción, las cuales van de la mano con la práctica de visualización y medición de las velocidades medias mencionadas. En la práctica de aproximación se deben medir varias velocidades medias entre (1,1) y los puntos estimados, tomando cada vez puntos más cercanos a él; en la de predicción se elige una velocidad media (la mejor de ellas, calculada con el punto elegido más cercano a (1,1) y dicho punto), que permite establecer una conjetura del valor de la velocidad instantánea allí. La práctica de visualización permitió elegir los puntos base para las mediciones y predicciones. Se logró el propósito en todos los grupos
En el video 1 se ve cómo el grupo 1 (21:42) fundamentó su respuesta a la presente pregunta a través del siguiente argumento: a medida que se tomen puntos cada vez más cercanos al (1,1) en la gráfica de f(t) y se calculen velocidades medias entre dichos puntos y el último, hay mejores aproximaciones a la velocidad instantánea en (1,1) a través de dichas velocidades medias. Se evidencia algo similar en el video 2, en donde aparece el grupo 4 (00:00), y en el video 3, cuando entran en escena los grupos 5 (00:30) y 6 (04:00)
A continuación, se aprecia en los documentos entregados por los estudiantes cómo los grupos 5 y 2, respectivamente: 1) eligieron puntos de la gráfica y asignaron el valor de sus componentes (práctica de visualización, localización y medición), 2) calcularon el valor de las velocidades medias entre dichos puntos y el punto (1,1) (práctica de medición), 3) realizaron una predicción del valor de la velocidad instantánea en el punto (1,1) por medio de la elección de una velocidad media de las calculadas (la correspondiente entre el punto (1,1) y (1.05, 1.05)), la cual es una buena conjetura de la instantánea, por cuanto el punto (1.05, 1.05) es muy cercano al (1,1). Este proceso nos da pie a deducir que la práctica de referencia de predicción acompañó la construcción de conocimiento de los estudiantes, junto con las prácticas socialmente compartidas ya mencionadas.
Es evidente el uso constante de los lenguajes numérico (junto con la práctica manejo de datos) y visual en lo que va del análisis de la actividad. El grupo 2 escogió puntos por la derecha y por la izquierda del punto (1,1) para realizar una predicción de la velocidad instantánea en dicho punto.
La pregunta 4 fue crucial en la presente actividad, puesto que apuntó a la construcción del concepto de derivada en un punto a través de su equivalente, el de velocidad instantánea. El objetivo se logró; todos los grupos explicaron la velocidad instantánea en un punto como el paso al límite en el tiempo de la velocidad media entre dicho punto y otros de la gráfica, ya que habían desarrollado una idea de este concepto en una actividad previa, como se muestra a continuación (grupo 5). Es de notar que dicho grupo llegó a la conclusión anterior en el video 3 (09:10), en donde hubo problemas en la escritura de esta en cuanto modelo, los cuales fueron superados posteriormente (video 3, 15:15). Se advierte también la tentativa del grupo de utilizar el concepto límite en la presente pregunta. La práctica social del praediciere se deduce de lo hablado hasta ahora, en donde en este punto el concepto que se está trabajando en el salón de clase se condensa en un modelo (práctica de modelación y representación), que nos permite plasmar la predicción objeto de la actividad; este modelo se construye también con ayuda de la práctica manejo de datos. También, con la construcción de un modelo matemático para la velocidad instantánea se puede deducir la entrada en escena de la práctica de referencia de la algebrización, como componente de la práctica social del praediciere.
El grupo 1 tuvo inconsistencias cuando afirmó que la aproximación no se puede graficar ni escribir, sin embargo se llegó a la escritura de una expresión que involucra el límite de la velocidad media mencionada. En el video 3 (24:29) se nota cómo dicho grupo llegó a la conclusión escrita abajo.
Una idea intuitiva de aproximación fue empleada parcialmente por algunos de los estudiantes en sus diálogos para construir el concepto de velocidad instantánea en un punto, junto con las prácticas mencionadas con anterioridad. Por ejemplo, en el video 3 se usó la fórmula clásica de velocidad instantánea para responder a la pregunta:  ; la fórmula fue aprendida por un integrante del grupo previamente de forma memorística, ya que no se daba cuenta del sentido de los elementos que aparecían en ésta (19:27); pero con la ayuda de la presente actividad y con el énfasis de esta en las prácticas y prácticas de referencia citadas como acompañantes en la construcción de conocimiento, el estudiante pudo aprender de una forma más significativa.
; la fórmula fue aprendida por un integrante del grupo previamente de forma memorística, ya que no se daba cuenta del sentido de los elementos que aparecían en ésta (19:27); pero con la ayuda de la presente actividad y con el énfasis de esta en las prácticas y prácticas de referencia citadas como acompañantes en la construcción de conocimiento, el estudiante pudo aprender de una forma más significativa.
En la presente pregunta fue necesario construir un modelo (práctica de modelación) de la velocidad instantánea en (1,1), puesto que mediante el lenguaje numérico se llega sólo a presunciones de tal velocidad por medio de la medición de velocidades medias. El modelo apareció en la actividad de forma natural, como en los grupos anteriores, en donde el lenguaje algebraico y la noción de límite (construida en una actividad anterior) llevaron a la cimentación de una fórmula para la velocidad instantánea en (1,1), la cual condensa “la mejor aproximación a dicha velocidad”.
En la pregunta 5 se pidió a los estudiantes que trazaran rectas secantes a la gráfica de f(t) con base en los puntos (1,1) y los elegidos en la pregunta 3, con los cuales se hallaron las aproximaciones a la velocidad instantánea en (1,1) (práctica de representación y graficación).
Nos enfocaremos ahora en la actividad plenaria. Un estudiante leyó la pregunta 6 a la clase; en seguida otro participó contestando a la pregunta, argumentando que geométricamente la velocidad instantánea en un punto significa la pendiente de la recta tangente a dicha gráfica en tal punto. El profesor clarifica en el tablero lo mencionado por el estudiante, mostrando cómo a medida que se toman puntos más próximos al (1,1) en la gráfica de f(t), las rectas secantes formadas por dichos puntos y el (1,1) tienden a ser la recta tangente a la gráfica en dicho punto.
En conclusión, las interacciones en el aula dan cuenta de que la actividad partió de la fórmula de la velocidad media entre dos puntos de una función de trayectoria, junto con el hecho de que dicha velocidad geométricamente es la pendiente de la recta secante que pasa por dichos puntos; por otra parte, se terminó con la construcción de un modelo para la velocidad instantánea en un punto de una trayectoria, junto con la construcción del hecho de que tal velocidad es la pendiente de la recta tangente a la trayectoria en tal punto. Además, el trabajo realizado por los estudiantes a partir de la actividad en el aula fundamentada en la SE permitió que ellos desarrollaran habilidades importantes del pensamiento matemático, tales como esquematizar, formular y visualizar un problema de diferentes maneras, predecir situaciones, descubrir relaciones y regularidades, tal como Camacho (2006) afirma con relación a intervenciones socioepistemológicas.
CONCLUSIONES
Prácticas socialmente compartidas, tales como visualización, medición, manejo de datos, aproximación, clasificación, narración, comparación, estimación, representación, interpretación, justificación, localización, explicación, graficación, que fueron base para la formulación de la actividad, acompañaron la construcción del concepto de derivada de una función en el punto (1,1); así se posibilita un puente entre el conocimiento particular y el generalizado; la actividad también se fundamentó en las prácticas de referencia temporalización, secuenciación, algebrización y predicción.
Una idea intuitiva de aproximación fue empleada parcialmente por algunos de los estudiantes en sus diálogos para construir el concepto de velocidad instantánea en el punto (1,1), junto con las prácticas mencionadas con anterioridad.
El trabajo realizado por los estudiantes a partir de la actividad en el aula fundamentada en la SE permitió que ellos desarrollaran habilidades importantes del pensamiento matemático, tales como esquematizar, formular y visualizar un problema de diferentes maneras, predecir situaciones, descubrir relaciones y regularidades.
La actividad descrita presenta un marco de referencia en cuanto a la enseñanza del concepto mencionado, cuya construcción se analizó con base en las prácticas socialmente compartidas involucradas en éste, como el destilado de la evolución pragmática (acción-actividad-práctica: práctica socialmente compartida); lo anterior debido a una crítica del discurso Matemático Escolar respecto al mencionado concepto.