La necesidad de la reorganización redaccional de los enunciados de problemas sobre la función logarítmica propuestos en textos escolares para mejorar su comprensión*

Nelson Javier Goyes Bastidas

Egresado de la Maestría en Enseñanza de las Ciencias Exactas y Naturales, Universidad Nacional de Colombia
https://orcid.org/0009-0002-3128-2867

Teresa Pontón Ladino

Coordinadora de la Maestría en Enseñanza de las Ciencias Exactas y Naturales, Universidad Nacional de Colombia
https://orcid.org/0000-0003-2399-7715

Recepción: 03 de abril 2023 | Aceptación: 14 de noviembre de 2023 | Publicación: 28 de febrero de 2024

DOI: http://dx.doi.org/10.18175/VyS15.1.2024.3

RESUMEN

Presentamos elementos de reflexión que permiten acercarse al papel de la organización redaccional frente a la comprensión de algunos enunciados de problemas que modela una función logarítmica propuestos en textos escolares. El objetivo principal es analizar el papel que cumple la reorganización redaccional en enunciados de problemas relacionados con la función logarítmica, elementos semióticos que permiten promover la articulación de los registros de representación semiótica, que pueden emplear los estudiantes para dar soluciones a las preguntas que se les propongan, dado que la comprensión de los enunciados de problemas radica en la coordinación de al menos dos registros de representación, pero parte de este registro de la lengua natural. En el diseño metodológico fue un estudio de caso de tipo cualitativo descriptivo, en el que se llevó a cabo la reorganización redaccional de cuatro enunciados de problemas sobre la función logarítmica, seleccionados de tres textos escolares. Dichos enunciados se aplicaron a siete estudiantes universitarios, con el fin de analizar sus producciones, tratamientos matemáticos y la forma en la cual articularon los distintos registros semióticos para dar solución al enunciado problema presentado. En relación con el desarrollo de la secuencia de enunciados se confirmó la necesidad de reformular los enunciados de problemas que conlleven la discriminación de todos los valores visuales del registro gráfico en correspondencia con las variaciones de las unidades significantes del registro algebraico.

PALABRAS CLAVE

función logarítmica, registros de representación semiótica, coordinación de registros de representación, actividades cognitivas, enunciados de problemas.

The Need for Editorial Reorganization of Problem Statements on the Logarithmic Function Proposed in School Textbooks to Improve Their Comprehension

ABSTRACT

We present elements of reflection that allow us to approach the role of the editorial organization in understanding certain problem statements modeled by a logarithmic function proposed in school texts. The main objective is to analyze the role that editorial reorganization plays in problem statements related to the logarithmic function, semiotic elements that promote the articulation of the semiotic representation registers that students can use to provide solutions to the proposed questions, since the understanding of problem statements lies in the coordination of at least two representation registers, but part of this is within the Natural Language register. The methodological design was a descriptive qualitative case study in which the editorial reorganization of four problem statements about the logarithmic function, selected from three school texts, was carried out. These statements were applied to seven university students in order to analyze their productions, mathematical treatments, and the way in which they articulated the different semiotic registers to provide a solution to the presented problem statement. In relation to the development of the sequence of statements, the need to reformulate problem statements that lead to the discrimination of all visual values in the graphic register in correspondence with variations in the significant units of the algebraic register was confirmed.

KEYWORDS

logarithmic function, semiotic representation registers, coordination of representation registers, cognitive activities, problem statements.

A Necessidade de Reorganização Redacional das Questões sobre a Função Logarítmica Propostas em Textos Escolares para Melhorar sua Compreensão

RESUMO

Apresentamos elementos de reflexão que permitem abordar o papel da organização redacional na compreensão de alguns enunciados de problemas modelados por uma função logarítmica proposta em textos escolares. O objetivo principal é analisar o papel desempenhado pela reorganização redacional nos enunciados de problemas relacionados à função logarítmica, elementos semióticos que promovem a articulação dos registros de representação semiótica que os alunos podem usar para responder às perguntas propostas, uma vez que a compreensão dos enunciados de problemas reside na coordenação de pelo menos dois registros de representação, incluindo o registro da língua natural. O design metodológico consistiu em um estudo de caso qualitativo descritivo, no qual a reorganização redacional de quatro enunciados de problemas relacionados à função logarítmica foi realizada, selecionados a partir de três textos escolares. Esses enunciados foram aplicados a sete estudantes universitários, a fim de analisar suas produções, tratamentos matemáticos e como eles articularam os diferentes registros semióticos para resolver o problema apresentado. Em relação ao desenvolvimento da sequência de enunciados, foi confirmada a necessidade de reformular os enunciados de problemas de forma a discriminar todos os valores visuais do registro gráfico correspondentes às variações das unidades significativas do registro algebraico.

PALAVRAS-CHAVE

Função logarítmica, registros de representação semiótica, coordenação de registros de representação, atividades cognitivas, enunciados de problemas.

Introducción

El estudio de las funciones logarítmicas tiene importancia para el desarrollo del pensamiento matemático, lo cual es reconocido en los Lineamientos Curriculares (1998) y Estándares Básicos de Competencias en Matemáticas2 (2006); en éstos se contempla el trabajo con ecuaciones cuadráticas, funciones, funciones exponenciales y funciones logarítmicas en el ciclo de los grados 8º y 9º, y nos plantean que los estudiantes deben alcanzar la competencia matemática de resolver problemas que involucran modelos exponenciales y logarítmicos.

En los Estándares Básicos de Competencias también se plantea la relevancia de trabajar con los registros semióticos de representación para la construcción de los conceptos matemáticos, donde se resalta “utilizar diferentes registros de representación o sistemas de notación simbólica para crear, expresar y representar ideas matemáticas; para utilizar y transformar dichas representaciones y, con ellas, formular y sustentar puntos de vista” (MEN, 2006, p.51).

De la misma forma, el National Council of Teachers of Mathematics (2000) indica que para desarrollar las competencias de los estudiantes en la resolución de problemas, razonamiento, comunicación, entre otros, se recomienda una serie de estrategias que se pueden implementar en el currículo escolar: seleccionar y usar varios tipos de razonamientos y métodos de prueba, analizar y evaluar el pensamiento matemático propio y las estrategias de otros, entender cómo las ideas matemáticas se interconectan, y estrategias de correspondencias entre las representaciones matemáticas para resolver problemas.

Ahora bien, por mucho tiempo ha sido recurrente identificar en diferentes investigaciones que los procesos de comprensión de los enunciados de problemas en área de matemáticas generan altos niveles de dificultad en los estudiantes. Es común encontrar en distintas pruebas internas y externas, que evalúan diferentes procesos dentro de la construcción del conocimiento matemático, resultados que indican o sugieren este tipo de dificultades (Duval, 1999; Pontón, 2012). Cabe resaltar que, en el mismo estudiantado en general y en el ambiente cultural, se ha construido la idea que el conocimiento matemático es difícil de adquirir, especialmente cuando está relacionado con la resolución de problemas.

Al respecto, algunos autores han analizado la dificultad en la enseñanza y el aprendizaje sobre el concepto de función a partir de distintas perspectivas. En primer lugar, encontramos a Planchart (2002); en su tesis doctoral, titulada “La visualización y modelación en la adquisición del concepto de función”, se propuso identificar y analizar las dificultades en el proceso de aprendizaje del concepto de función en los estudiantes, tema básico del curso de Precálculo en Puerto Rico.

En esta investigación se evidenció la dificultad que tienen los estudiantes para escribir la representación algebraica de una función que previamente habían graficado, y que algunas imágenes mentales asociadas al concepto de función prevalecen en el aprendizaje de los estudiantes. Esto se debe a que, como propone Planchart (2002), “los estudiantes tendieron a encasillarse en un término o a una imagen visual-textual. Los estudiantes utilizaron con frecuencia la palabra ‘único’ o ‘solo’ que aparece dominante en la definición de función” (pág. 165). En el caso del registro tabular, los estudiantes respondían a un patrón o una ecuación.

En segundo lugar, Guzmán (1998), apoyado en la teoría de Duval, les preguntó a estudiantes que cursaban el primer año de ingeniería sobre ciertas nociones asociadas al concepto de función, con referencia a los registros gráficos, algebraico y en lengua natural. Este estudio reveló que hay una ausencia de articulación entre las diferentes representaciones semióticas del concepto de función, dado que las respuestas de los estudiantes solían presentarlas en el mismo registro en el cual se había propuesto la pregunta (monorregistros); a veces recurrían al sistema semiótico simbólico algebraico, y en muy pocas ocasiones acudían a otro sistema de representación auxiliar.

En tercer lugar, Duval (1988a) realiza en Francia la indagación “gráficas y ecuaciones”; con esta aplica una breve prueba a estudiantes de primero de preparatoria durante el primer trimestre, en la cual debían identificar y relacionar gráficas de funciones lineales con sus correspondientes ecuaciones. Los resultados evidenciaron que los estudiantes presentan dificultades para hacer conversiones del registro gráfico cartesiano al simbólico algebraico; esto se debe a que la mayoría de los estudiantes eligieron la vía del punteo para dar solución a dicha prueba. La razón de ello obedece al desconocimiento de las reglas de correspondencia semiótica que existen entre las representaciones gráficas cartesianas y simbólicas algebraicas, y a los fenómenos de no congruencia entre los distintos registros de representación.

Las dificultades de comprensión en los estudiantes obedecen a aspectos relacionados no sólo con el contenido enseñado (enunciados de problemas, conceptos de funciones, entre otros), sino con la elaboración de conceptos y nociones propios del cálculo diferencial e integral; con escribir la representación simbólica algebraica dada su representación gráfica cartesiana, o realizar la conversión de la representación gráfica cartesiana a la representación simbólica algebraica; con identificar relaciones matemáticas en el contexto extramatemático de los enunciados de problemas de la función logarítmica y poder establecer las representaciones semióticas en éstos.

En razón de ello, algunos investigadores, como Duval (2006), Guzmán (1998), Planchart (2002) y Pontón (2008), en las últimas décadas han intentado explorar nuevos caminos de orden didáctico y cognitivo que permitan superar o hacer más comprensible el conocimiento matemático, específicamente, en el análisis y resolución de problemas que se proponen en el aula de clases.

En ese mismo sentido, este artículo3 tiene el interés de analizar el papel de la reorganización redaccional en enunciados de problemas relacionados con la función logarítmica, para propiciar la articulación de registros de representación semiótica, y, así, contribuir a la comprensión de éstos. Para lo anterior, se seleccionaron algunos enunciados de problemas de la función logarítmica propuestos en tres textos escolares colombianos, a los que se les realizaron las respectivas variaciones redaccionales con el fin de identificar el papel que cumplen éstas en la comprensión de los enunciados.

Cabe mencionar que en toda actividad matemática se debe llevar a cabo la coordinación de distintos registros de representación semiótica sobre el objeto matemático que se estudia. Empleando las palabras de Duval (2006):

Desde un punto de vista matemático, la conversión y el tratamiento son un todo en la resolución de problemas. Es más, lo que importa es el tratamiento que es el que hace relevante la elección del “mejor” cambio de registro (economía de medios, más potencia para la generalización, o más intuitivo...) para resolver el problema dado. (p. 149)

Es por esto que, en la reorganización de los enunciados de problemas de la función logarítmica, es fundamental la articulación de distintos registros de representación para su comprensión y resolución. Dicha comprensión es producto de la conversión de las representaciones de los objetos matemáticos.

Por consiguiente, es necesario proponer a los estudiantes enunciados de problemas en los que puedan realizar tratamientos en distintos registros semióticos posibilitando la articulación con otros sistemas de representación (lengua natural, registro gráfico cartesiano, registro simbólico algebraico o tabular).

Ahora bien, cuando se realiza la reorganización redaccional de las unidades segmentadas de un texto, se permite al lector identificar o adquirir una aprehensión global y precisa del texto, los temas principales, el orden de presentación de los elementos explicitados y los detalles significativos. Esta reorganización se puede llevar a cabo de dos formas: una cognitiva y la otra redaccional. Respecto a la reorganización cognitiva, Duval (1999) afirma que “moviliza esencialmente los conocimientos relativos a las situaciones, a los objetos o a las preguntas que el texto evoca, o que trata, independiente de lo que la redacción del texto explicita” (p. 278). En relación con la reorganización redaccional, se puntualiza que “es la operación que explicita todas las relaciones que tiene entre sí las unidades discriminadas por segmentación funcional… El conjunto de estas relaciones constituye la organización redaccional del texto” (Duval, 1999, p. 278).

La organización redaccional del enunciado de un problema está determinada por las estrategias utilizadas por el autor para que el posible lector, esto es, el estudiante, logre enfrentarse al enunciado del problema. Esto implica que reconozca el contexto extramatemático, identifique la información matemática, las relaciones matemáticas entre estas informaciones numéricas, las marcas o informaciones relevantes, que le permitan al estudiante hacer las transformaciones en el interior de cada registro, partiendo del registro de la lengua natural y, así, llegar a una objetivación del conocimiento movilizado.

Según Duval (1999), en las variables de la redacción se pueden distinguir tres factores que inciden en la variación redaccional de un texto. El primer factor hace referencia a la explicitación de aquellos elementos de contenido cognitivo que son utilizados en el enunciado de un problema. El segundo factor corresponde a la selección de aquellas expresiones que se deben especificar en el enunciado del problema, y el tercer factor concierne al orden en que se presentan las expresiones que son explicitadas en el enunciado del problema.

En el caso de los enunciados de problemas que introducen la función logarítmica, se requiere que el lector identifique características semánticas, aspectos físicos y conceptuales, relaciones entre representaciones tabulares, gráficas cartesianas o simbólicas algebraicas propias de este campo de enunciados, a partir de los diferentes registros.

De acuerdo con lo anterior, conviene subrayar que este estudio de investigación está enmarcado en la teoría semiótica cognitiva desarrollada por Duval (1988a, 1988b, 1999, 2004, 2006, 2017) y la teoría semiótica cognitiva y lingüística planteada por Pontón (2008, 2012). A partir de estas bases teóricas se analizó el papel que tienen los cambios de redacción en enunciados de problemas sobre la función logarítmica, de tal manera que favorecieran la articulación de registros de representación semiótica para contribuir a una mejor comprensión de estos.

Gracias a estas teorías se comprende que en toda actividad matemática se debe llevar a cabo la coordinación de distintos registros de representación semiótica sobre el objeto matemático que se estudia. En este caso, en los enunciados de problemas de la función logarítmica, es fundamental la articulación de distintos registros de representación para su comprensión, producto de la conversión de las representaciones de los objetos matemáticos.

En consecuencia, el objeto de estudio se centró en analizar el papel que cumple la reorganización redaccional en enunciados de problemas relacionados con la función logarítmica, para propiciar la articulación de registros de representación semiótica y, así, contribuir a la comprensión de estos. La razón por la cual el presente trabajo se centra en la función logarítmica obedece a que, justamente, dicha función es la que menos trabajos de investigación se han preocupado de abordar, pues se encontraron suficientes referencias respecto a funciones lineales, cuadráticas, e incluso exponenciales, mas no como tal de la función logarítmica.

En lo que respecta a la implementación del diseño metodológico de investigación, se realizó un estudio de caso de tipo cualitativo descriptivo, en el que se llevó a cabo la reorganización redaccional de dos enunciados de problemas sobre la función logarítmica, seleccionados de tres textos escolares. Dichos enunciados seleccionados se propusieron a siete estudiantes universitarios de primera matrícula, con el fin de analizar en sus producciones las transformaciones entre las representaciones realizadas y la forma en la cual reorganizaron los elementos que les permitieron articular los distintos registros semióticos para dar solución a los enunciados de problemas.

Fundamentación teórica de la función logarítmica a partir de una mirada semiótica cognitiva y lingüística

La importancia de los sistemas semióticos de representación radica no sólo en la designación entre los objetos matemáticos, sino especialmente en sus amplias posibilidades de transformación. Toda transformación o actividad matemática requiere utilizar un sistema semiótico de representación, como lo afirma Duval (2006):

No se reduce a designar objetos, a ponerse en lugar de algo, o a ser ellas mismas consideradas como objetos. Su uso está determinado por la posibilidad del procesamiento matemático que permiten. Cualesquiera sean las representaciones semióticas usadas, se pueden cambiar por otras representaciones semióticas sin el apoyo de nuevos datos u observaciones empíricas. (p. 69)

En toda actividad matemática en la que se involucran cambios de registros de representación, Duval (1999) plantea tres actividades cognitivas inherentes a toda representación. La primera actividad cognitiva es la formación de una representación semiótica, la cual corresponde al conjunto de marcas perceptibles e identificables que se pueden expresar o evocar de un objeto como una representación en un sistema semiótico determinado.

La segunda actividad cognitiva es el tratamiento, que consiste en las transformaciones de la representación que ocurren dentro del mismo registro semiótico en el que se ha formado, obedeciendo a las reglas propias del mismo sistema, de tal modo que las representaciones que se obtengan pueden constituirse como un conocimiento.

La tercera actividad cognitiva corresponde a la conversión, la cual consiste en la transformación de la representación inicial en otra representación de otro registro en la que se conserva la totalidad o parte del significado de la representación dada. Es otras palabras, que, al realizar las transformaciones a otros registros, se obtienen nuevas significaciones del objeto que se representa. Duval (2016) afirma que:

La conversión, que es una transformación en la representación, es más compleja que el tratamiento porque cualquier cambio de registro requiere primero que entre dos representaciones cuyos contenidos con frecuencia no tienen nada en común, se reconozca al mismo objeto representado. (p. 75)

Por su parte, Pontón (2012) resalta que la comprensión de enunciados de problemas no es una tarea sencilla de enseñanza y aprendizaje, dado que, si se toman en consideración las implicaciones cognitivas que en esta subyacen, van más allá de ciertos algoritmos y pasos para llegar a la solución de los problemas. Involucra tanto tareas de conversión de un registro semiótico a otro como la discriminación de las unidades significantes, dado que éstas, además de permitir al estudiante el reconocimiento de los elementos para el proceso de comprensión de los enunciados de problemas matemáticos, determinan la congruencia y no congruencia entre la conversión de un registro de representación a otro.

A partir de este punto de vista, la comprensión de los problemas en matemáticas no sólo depende de las reglas de la lengua natural, sino también de la organización de los objetos matemáticos y de la situación extramatemática a la cual se refiere, al igual que los conocimientos previos que posean los estudiantes.

En el caso del campo de enunciados de la función logarítmica, la comprensión de problemas de dicha función implica reconocer en el enunciado, cada una de las unidades segmentadas de información, en articulación con la pregunta y la respuesta que se busca en cada una de ellas. Pontón (2012) menciona que:

La selección de los datos pertinentes para la resolución del problema y la elaboración de una representación auxiliar cuya función sea la de facilitar el paso del enunciado al tratamiento aritmético son dos acciones básicas para la comprensión de un enunciado de problemas por parte de un estudiante, las cuales dependen de la congruencia entre la presentación de la redacción del enunciado y el tratamiento aritmético que se debe efectuar en el registro semiótico apropiado. (p. 457)

Si se considera el esquema del análisis global de la estructura de los enunciados de problemas, Pontón (2012) resalta que se pueden identificar los actos de habla de tipo aseverativo y directivo. Las aseveraciones son todas las unidades de información que afirman algo en el enunciado del problema, y los directivos son aquellas unidades de información que permiten reconocer la relación entre las unidades de información que afirman algo y lo que se pide en la pregunta directa o indirecta.

Pontón (2012) argumenta que en “el campo de enunciados de problemas, la comprensión puede enfocarse sólo a uno de los dos lados del discurso, por un lado, a la organización de la redacción y, por otro lado, a la del objeto que se trata” (p. 412).

En este caso, es necesario proponerles a los estudiantes enunciados de problemas en los que se posibilite efectuar transformaciones de la función logarítmica, a partir de aprehensiones globales cualitativas de las variables visuales en la representación gráfica cartesiana. Es otras palabras, que los estudiantes puedan llevar a cabo tratamientos en distintos registros semióticos, mediante la articulación con otros sistemas de representación (gráfico cartesiano y simbólico algebraico).

Para articular los distintos registros semióticos, Duval (1999) define las variables visuales y categoriales como un “sistema particular de signos: el lenguaje, la escritura algebraica o los gráficos cartesianos, y en que pueden ser convertidas en representaciones semióticas ‘equivalentes’ en otro sistema semiótico” (p. 27). Es decir, que las variables visuales son todas las modificaciones de la representación gráfica cartesiana que generan una modificación en la escritura simbólica o expresión algebraica. En cuanto a las variables categoriales de las representaciones simbólicas algebraicas de la función logarítmica, corresponden a los términos en su escritura algebraica que expresan las características de la función como los desplazamientos, cortes, crecimientos y asíntotas.

Por ejemplo, si al estudiante se le propone el siguiente enunciado del problema: “la función que modela el número de ventas de automóviles deportivos con respecto al tiempo es: f(t)=0,98 -1,97 log (t+1). Contesta: ¿Qué podrías decir del comportamiento del número de ventas de automóviles deportivos? ¿Qué representa el signo negativo que se constituye en 1,97 log (t+1) ?”.

En el anterior enunciado del problema se espera que el estudiante identifique, ilustre y caracterice la representación gráfica cartesiana de la nueva modelación de la función logarítmica y obtenga información sobre la interpretación global del comportamiento de la función en el contexto de la situación del problema. Con esto se busca que el estudiante logre visualizar cómo se modifican las variables visuales del gráfico cartesiano articulado con las variables categoriales de la escritura simbólica algebraica.

Conviene aquí detenerse, para analizar en la figura 1 las variables visuales que los estudiantes deben discriminar y hacerlas corresponder con las variaciones en los símbolos de la representación simbólica algebraica.

Figura 1. Articulaciones con la representación gráfica cartesiana y simbólica algebraica de la función
f (x) =0.98 - 1.97 log (t+1)

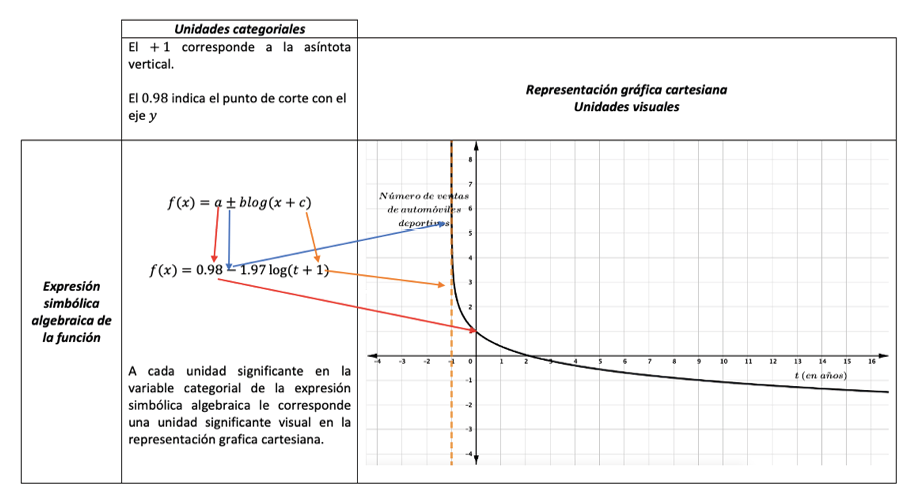
Fuente: Goyes (2021, p. 28).

Como se muestra en la figura 1, los estudiantes deben hacer corresponder las variables categoriales en la escritura simbólica algebraica con las variables visuales de la representación gráfica cartesiana de la función. Lo que quiere decir que, en la variable categorial de la representación simbólica algebraica f(t)=0.98 - 1.97 log (t+1), el término independiente representa el punto del corte con el eje (véanse las flechas de color rojo en la figura 1), que corresponde a una unidad significante visual en la representación gráfica cartesiana que permite inferir que a partir del punto de corte con el eje comienza a descender el número de ventas de los automóviles.

El signo negativo que antecede en el coeficiente log(t + 1) indica que la función es decreciente en su dominio y que el coeficiente impacta en la representación gráfica cartesiana de la función provocando que las parejas coordenadas en el plano cartesiano crezcan de manera lenta (véanse las flechas de color azul en la figura 1). Además, en log(t + 1) el valor numérico indica la asíntota vertical de la función (véanse las flechas de color naranja en la figura 1).

Por tanto, las variables visuales y categoriales determinan las características de la función logarítmica como los desplazamientos, cortes, crecimientos y asíntotas que dan cuenta del reconocimiento de cambios visuales en la representación gráfica cartesiana y de sus relaciones de covariación que se presentan en la escritura simbólica algebraica.

Duval (1999) resalta que la aprehensión global cualitativa permite visualizar las características de una función en una representación gráfica cartesiana para identificar y reconocer las relaciones de variación en la representación simbólica algebraica. En ese sentido, Duval (2006) menciona que “la toma de conciencia de la especificidad de estos tratamientos visuales por parte de los alumnos es una condición previa y necesaria para la resolución de problemas” (p. 149).

En la figura 2 se identifican las variables visuales y sus correspondientes unidades simbólicas de la función logarítmica y = a logb(x+h)+k donde se logra reconocer las posibles variaciones de los parámetros de dicha función, que permite la expansión de expresiones simbólicas algebraicas, que modifican la función y su representación gráfica cartesiana.

Figura 2. Variaciones visuales de la función logarítmica y = a logb(x+h)+k

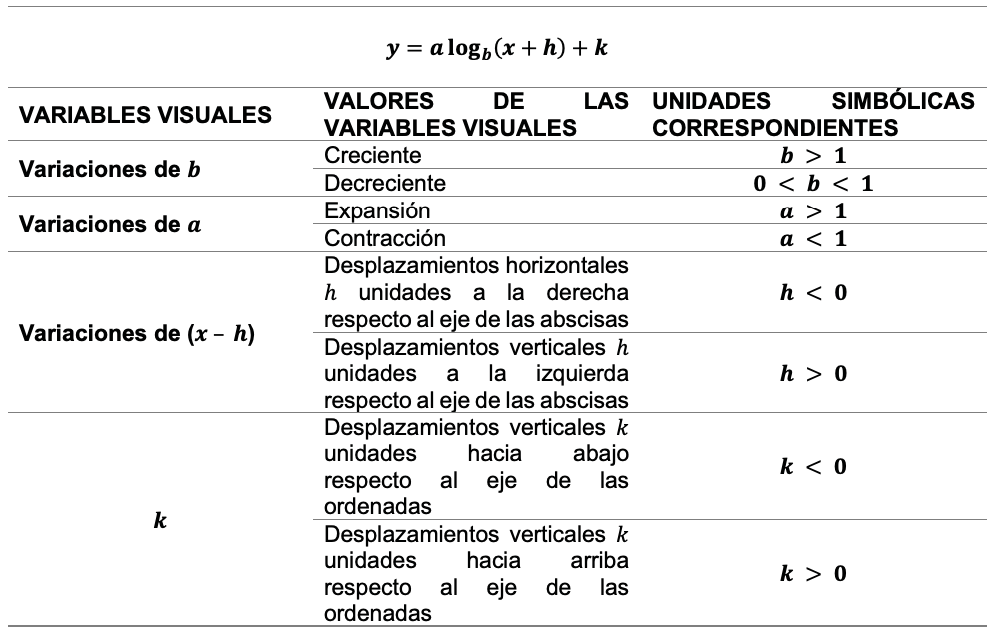
Fuente: Goyes (2021, p.30).

Una vez definidas las variables visuales y simbólicas correspondientes, puede verse que son necesarias para que el estudiante logre razonar y visualizar el comportamiento de una función logarítmica, y, así, logre articular las representaciones gráficas cartesianas con las simbólicas algebraicas, y viceversa.

Con relación a la comprensión de los enunciados de problemas de la función logarítmica a partir de los distintos registros de representación, gran parte del análisis se debe centrar en identificar aquellas unidades significantes presentes en los registros gráficos cartesianos y simbólica algebraica. Es por ello que, en la conversión de la representación gráfica cartesiana a la escritura de la representación simbólica algebraica, y viceversa, es primordial que se identifiquen aquellas variables visuales pertinentes en el gráfico cartesiano en relación con sus diferentes valores categoriales en la representación simbólica algebraica. Así mismo, que se discriminen aquellas unidades significantes propias de cada registro.

Ahora bien, en los enunciados de problemas que involucran la función logarítmica, la segmentación corresponde a unidades textuales de información que permiten al estudiante llegar a una mejor comprensión del objeto matemático en estudio. De acuerdo con lo planteado por Duval (2004), la segmentación en unidades que se realiza de un texto, o de un enunciado del problema matemático, posibilita que en cada unidad discursiva segmentada se pueda efectuar un tratamiento de orden semántico o cognitivo sobre las marcas lingüísticas (matemáticas o propias del contexto extramatemático); en otras palabras, esta segmentación descompone el texto en unidades textuales de información, con las que se busca que los estudiantes empiecen explícitamente a relacionarlos, para entender las relaciones, las cantidades en el marco del contexto de la situación problema (extramatemática).

En la figura 3 se puede analizar un enunciado del problema acerca de la mortalidad infantil en el contexto de Estados Unidos, con el fin de ejemplificar la segmentación de un texto de acuerdo con las informaciones dadas en el texto.

Figura 3. Ejemplo de un enunciado de problema de función logarítmica

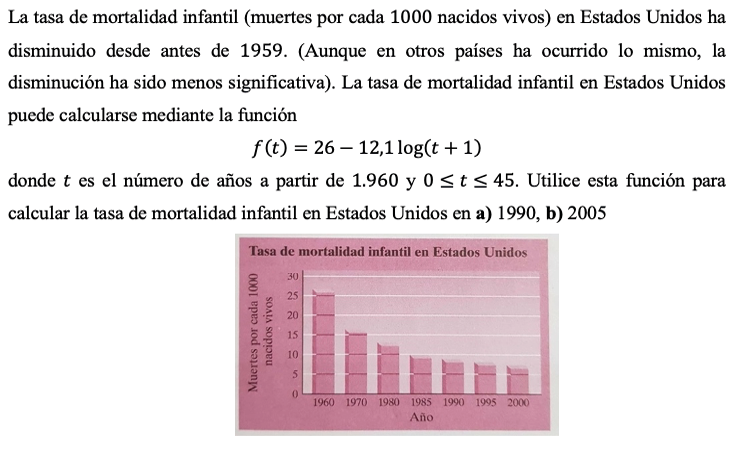
Fuente: tomado de Ángel (2004, p. 651).

En la figura 4 se observa una posible segmentación de las informaciones dadas por el enunciado de la figura 3 y la articulación con la pregunta que se plantea, en las que se resaltan con rojo algunas de las marcas lingüísticas que establecen un significado en la articulación de los segmentos del enunciado.

Figura 4. Segmentación de las unidades enunciativas directas dadas
en el enunciado del problema de retención de conocimientos

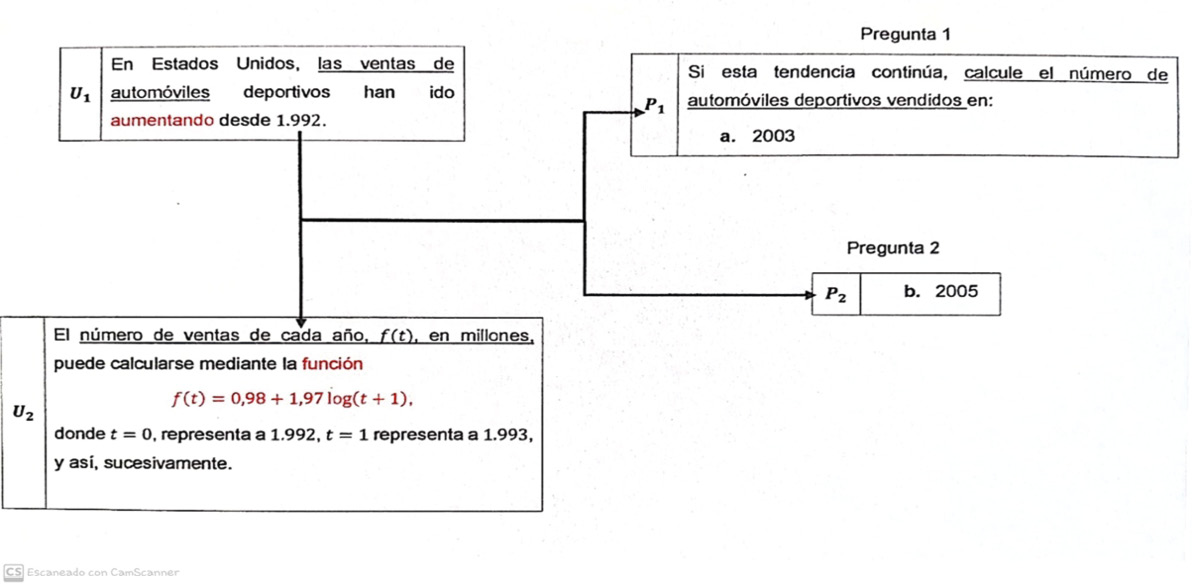
Fuente: Goyes (2021, p. 39).

En la figura 4 se muestra que en el enunciado propuesto se establecen relaciones entre las variables: tasa de mortalidad infantil en función de los años transcurridos; como se puede observar en U1 y U2 las unidades de información U1 y U2 se asocian para responder a las preguntas explicitadas en lengua natural en P1 y P2.

Cabe agregar que la reorganización redaccional no es suficiente con la segmentación de las unidades del texto para la comprensión de un enunciado de problema; se hace necesario la variación de éste, con el fin de percibir las conexiones de las unidades de información y la organización redaccional del enunciado del problema para lograr la comprensión de éste.

Esta reorganización se puede llevar a cabo de dos formas: una cognitiva y la otra redaccional. En la cognitiva, se movilizan los conocimientos que el texto evoca en sus diferentes situaciones, preguntas u objetivos; en otras palabras, la recontextualización cognitiva es externa al texto (Duval, 1999). La redaccional establece las conexiones entre las unidades segmentadas (por la segmentación funcional) explicitando las relaciones que tienen entre sí, es decir, que la recontextualización redaccional es interna al texto (Duval, 1999).

Cuando se realiza una reorganización redaccional de las unidades segmentadas de un texto como el enunciado del problema, ésta debe permitirle al lector identificar o adquirir una aprehensión global y precisa del enunciado, las principales designaciones, relaciones, el orden de presentación de los elementos explicitados y los detalles significativos. En el caso de los enunciados de problemas que introducen la función logarítmica, esta reorganización debe permitirle al lector identificar características semánticas, aspectos físicos que se modelan y aspectos conceptuales propios de esta variación logarítmica, entre otros.

A continuación, en la figura 5 se presenta un ejemplo de un enunciado de problema de la función logarítmica, en el que se realizan algunas reorganizaciones redaccionales con el fin de llevar a la comprensión de éste.

Figura 5. Ejemplo de un enunciado del problema de función logarítmica

Fuente: tomado de Ángel (2004, p. 645).

Vamos a ver ahora la reorganización redaccional del enunciado de problema mostrado en la figura 5:

En Estados Unidos, las ventas de automóviles deportivos han ido aumentando a partir de 1992. El número de ventas de cada año, f(t), en millones, puede calcularse mediante la función f(t)= 0.98 + 1.97 log (t+1). La función se representa en el gráfico cartesiano de la figura 6.

Figura 6. Representación gráfica cartesiana de la función logarítmica f(t)= 0.98 + 1.97 log (t+1)

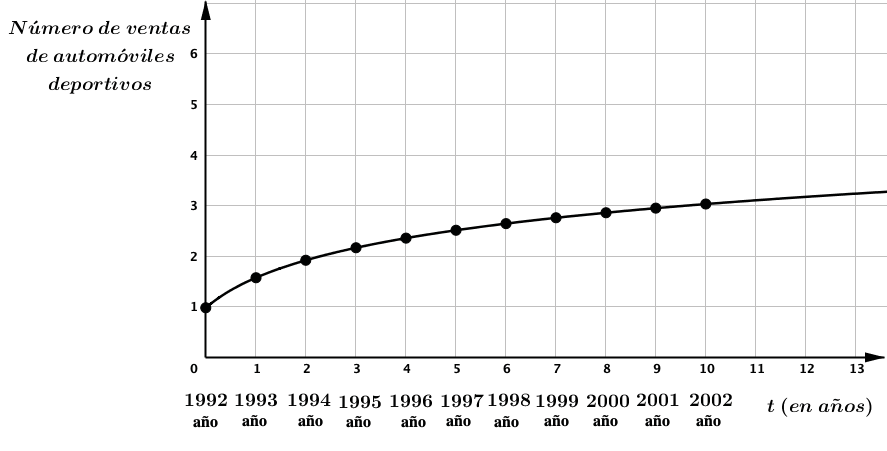
Fuente: Goyes (2021, p. 41).

En el enunciado del problema se les propone a los estudiantes preguntas como:

1. Según la representación gráfica cartesiana de la función f(t)= 0.98 + 1.97 log (t+1). A partir del año de referencia, ¿se puede afirmar que el aumento de automóviles deportivos crece de manera rápida a medida que transcurren los años? Explica tu respuesta.
2. ¿Cuál es la tendencia que se logra observar al pasar los años con las ventas de los automóviles deportivos?
3. ¿Cómo incide el signo positivo que antecede en 1.97log (t + 1)? ¿Qué pasaría si a la función se le antecede un signo negativo en 1.97log (t + 1)? ¿El número de ventas aumentaría? ¿Cómo crees que sería su representación gráfica cartesiana?

Con estas preguntas se busca que el estudiante, en el enunciado propuesto, pueda observar los elementos de las unidades significantes presentes en el registro gráfico cartesiano articulado con las unidades significantes en el registro simbólico algebraico de la función dada.

Cabe anotar que el registro en el que se presenta un enunciado de problema no garantiza su comprensión; tampoco la garantizan las habilidades lectoras que tenga el lector, dado que, para la comprensión de textos, y específicamente, para la comprensión de enunciados de problemas, puede generar dificultad la organización de la redacción del enunciado. A esto se suma que la comprensión de textos también depende de la base de conocimientos que tenga el lector en relación con el contenido cognitivo del texto (Duval, 1999).

Por lo tanto, se debe considerar que, para la comprensión de un enunciado de problema, es necesario tener en cuenta dos aspectos: el primero atañe a las variables de la redacción determinadas por la organización del enunciado, que depende de la interacción entre el contenido cognitivo de éste y su organización redaccional, siendo esta última determinada por las variaciones de la redacción; y el segundo aspecto está relacionado con las variables relativas al lector, las cuales abarcan la base de conocimientos, la comprensión del vocabulario y organización redaccional que puede realizar, entre otros elementos.

DiseÑo metodológico

De acuerdo con las particularidades de esta indagación centrada en el aprendizaje, se requirió considerar una metodología cualitativa, que se caracteriza por “identificar la naturaleza profunda de las realidades, su estructura dinámica, aquella que da razón plena de su comportamiento y manifestaciones” (Martínez, 2014, p. 128). En otras palabras, de acuerdo con este autor, en el momento de describir los procesos cognitivos y procedimentales de los siete estudiantes escogidos, esta metodología cualitativa permitió ir al detalle de sus procedimientos y tener cierta amplitud para describir los elementos que acercaron a los alumnos a la comprensión de los enunciados.

Este tipo de investigación corresponde a un estudio de caso de tipo cualitativo descriptivo, en el cual se analizaron las producciones para identificar transformaciones de un grupo de siete estudiantes de primera matrícula pertenecientes a carreras de ingeniería o administración, chicos de 17 a 20 años, de una institución universitaria pública, en el año 2020, que llevaron a cabo la lectura y posible resolución de los enunciados de problemas de la función logarítmica, a los cuales se les hicieron modificaciones redaccionales, buscando que, a partir de la articulación de distintos registros de representación semiótica, se logre una mejor comprensión de éstos.

Este enfoque metodológico, entonces, sirvió para indagar, caracterizar y analizar las producciones realizadas por los estudiantes, desde algunos elementos de orden semiótico, lingüístico y cognitivo en el campo de enunciados seleccionados de la función logarítmica. Por esta razón, se describieron los razonamientos que se esperaban de los estudiantes en la comprensión de los enunciados propuestos, intentando mostrar con esto que la aparición de tales razonamientos o comportamientos plausibles es producto de la puesta en práctica de los conocimientos contemplados por los enunciados.

En la selección del campo de enunciados representantes de la función logarítmica fue fundamental seleccionar tres textos escolares de Colombia, que fueran muy utilizados en universidades en los primeros semestres; se escogieron todos los enunciados donde el texto estuviera presente en una situación extramatemática, y que la situación pueda estar representada a través de un modelo de tratamiento matemático (Duval, 1999).

Este análisis se realiza a partir de la teoría de Duval (2004) sobre la comprensión de textos, en el que se estudiaron problemas de la función logarítmica a partir de sus elementos de orden semiótico, lingüístico y cognitivo, los cuales se han de tener en cuenta para la reorganización redaccional de los enunciados de problemas seleccionados que permitan la superación de algunas dificultades reportadas en el análisis de los representantes del campo de enunciados de problemas de la función logarítmica y sus reorganizaciones redaccionales discursivas.

Para llevar a cabo el análisis de las producciones de los estudiantes se tomaron como referencia dos macrocategorías basadas en los referentes teóricos desarrollada por Duval (1988a, 1988b, 1999, 2004, 2006, 2017) y planteadas por Pontón (2008, 2012). Dichas macrocategorías se orientaron en la transformación de distintos registros de representación semiótica necesarios para la comprensión de los enunciados del problema y la comprensión, por parte de los estudiantes, de las representaciones gráficas cartesianas, de acuerdo con los enunciados del problema.

Las anteriores macrocategorías fueron definidas desde el análisis por medio de rejillas de las producciones de los estudiantes (cuadernillos entregados) tomando en consideración su pertinencia para la ejecución del análisis. Esta pertinencia se observó porque en las elaboraciones de los estudiantes se encontraron articulaciones de distintos registros de representación semiótica; describieron características propias de la función logarítmica; visualizaron el comportamiento de la función logarítmica en correspondencia con las variables categoriales de la representación simbólica algebraica; establecieron correspondencias entre los elementos presentados en el enunciado del problema con la representación gráfica cartesiana, entre otros. Además, se analizó la variable lingüística en las producciones de los estudiantes considerando aquellas marcas que les permitieron acceder al proceso de comprensión de los enunciados de problemas propuestos.

La validación de los resultados se realizó tomando en consideración los elementos determinados desde el marco teórico, a partir del diseño de rejillas de análisis de los enunciados de problemas de la función logarítmica de los textos seleccionados, que permitiera identificar aquello elementos semióticos y lingüísticos que debían introducirse en la variación redaccional de éstos. Es decir, que la triangulación de los datos (con las producciones de los chicos, el marco teórico, desde las rejillas de análisis) da cuenta de cómo la aplicación de los instrumentos responde a las variaciones de la redacción que se plantearon en la modificación de los enunciados de problemas propuestos.

Los resultados obtenidos son el producto de las interpretaciones que se hacen a partir de la teoría semiótica cognitiva desarrollada por Duval (1988a, 1988b, 1999, 2004, 2006, 2016, 2017), en función de lo que expresa cada estudiante en los procesos de comprensión de los enunciados propuestos y la teoría semiótica-cognitiva y lingüística planteada por Pontón (2008, 2012), con el fin de determinar el papel que desempeñan las variaciones de la redacción del campo de los enunciados de problemas de la función logarítmica, para tener una mejor comprensión de ese campo de enunciados.

El desarrollo de la presente investigación incluyó varias fases, las cuales se resumen en el siguiente esquema:

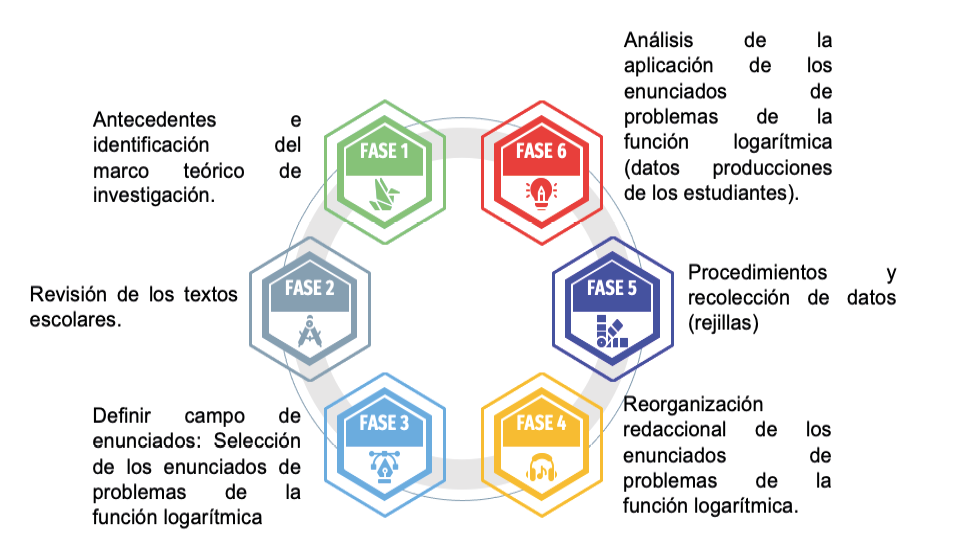
Fuente: creación propia.

análisis de los enunciados de problemas seleccionados de la función logarítmica y propuesta de variación redaccional

El análisis de los enunciados de problemas seleccionados se fundamenta en la noción de sistemas de representación semiótica, que focaliza su interés en identificar las formas de funcionamiento cognitivo necesarias para la producción de una actividad matemática, en el que se establece la necesidad de transformar los registros de representación semióticos de un sistema de representación a otro, que lleven a lograr la comprensión y el aprendizaje de las matemáticas.

Análisis del enunciado del problema 1: tasa de mortalidad infantil

En la figura 7 se observa que el enunciado del problema 1 se presenta en el registro semiótico de la lengua natural, acompañado de una representación simbólica algebraica; la situación que se enuncia está dada en el contexto del decrecimiento de la tasa de mortalidad infantil, y tiene una pregunta indirecta que conlleva plantear un tratamiento para dar una solución.

Figura 7. Presentación del enunciado del problema 1 (tasa de mortalidad infantil)

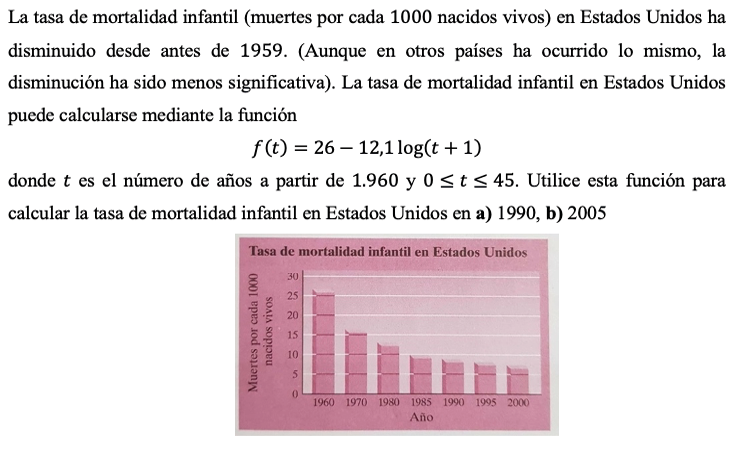
Fuente: tomado de Ángel (2004, p. 651).

En cuanto al aspecto lingüístico se refiere, en la figura 8 se presentan subrayadas unas posibles unidades segmentadas que relacionan información dada por el enunciado4 y la articulación con la pregunta formulada;5 además, se resaltan con rojo las marcas lingüísticas6 que establecen un significado con las unidades textuales de información en el enunciado del problema.

Figura 8. Segmentación de unidades textuales de la información dada en el enunciado
del problema 1 (tasa de mortalidad infantil)

Fuente: Goyes (2021, p. 89).

En la segmentación U1 , se debe cuestionar la concepción acerca del significado de la palabra “tasa” que va acompañada con la frase “mortalidad infantil”. En la figura 9 aparece la definición del término tasa.

Figura 9. Definición de tasa

Fuente: definición del término tasa, según la Real Academia Española (RAE).

El enunciado parte de la designación de la frase tasa de mortalidad infantil; se presupone que el estudiante asume como natural la comprensión de la designación “tasa”, pero en este enunciado se presuponen diferentes informaciones que tal vez no sean tan cotidianas o cercanas a los estudiantes. En la figura 10 se explicitan posibles presuposiciones que se alcanzan a generar de las segmentaciones textuales de información del enunciado del problema.

Figura 10. Algunas presuposiciones involucradas en las unidades segmentadas del
enunciado del problema 1 (tasa de mortalidad infantil)

Fuente: Goyes (2021, p. 91).

Como se puede observar en la figura 10, U1 y U2 y son relaciones que se establecen con el fin de responder a las preguntas explicitadas en lengua natural en P1 y P2. No obstante, no hay congruencia con las segmentaciones de las presuposiciones 1 y 2 establecidas con informaciones de las relaciones existentes entre las referencias seleccionadas en el enunciado y las preguntas. Esto se debe a que no hay congruencia con P1 y P2 en relación con U2 porque para averiguar la tasa de mortalidad infantil se debe utilizar la representación simbólica algebraica f(t)= 26 - 12.1 log (t + 1) cuando transcurren los años 1990 y 2005. Los años que se preguntan en P1 y P2 no se encuentran en función de años, sino en años transcurridos, así que no es posible que el lector sustituya en la representación de la función f(t)= 26 - 12.1 log (t + 1) el año 1990 o 2005 porque la representación simbólica algebraica está dada en función de (años).

En el enunciado del problema, el autor no expresa algunas presuposiciones como el registro auxiliar (ilustrativo) de “las representaciones de las alturas de las barras” que aluden al decrecimiento del número de muertes infantiles a medida que avanzan los años; el lector puede presuponer que el registro auxiliar (ilustrativo) no tiene ninguna relación con el enunciado porque “las barras” no están representando el gráfico cartesiano de la representación simbólica algebraica de la función logarítmica dada.

En este enunciado se identifican algunas dificultades, dado que no presenta las condiciones necesarias en U2 para dar respuesta a las preguntas P1 y P2, porque al autor del enunciado le corresponde comunicar al lector una correspondencia entre el año establecido y los años transcurridos. Es decir, en el año t = 0 representaría el año de 1960, y así, para el año 1970 habrán pasado 10 años, siendo t = 10, para lo cual en el enunciado se debería preguntar claramente en los años transcurridos a partir de 1960 hasta 1990 o darle explícitamente los años o involucrar esas marcas lingüísticas que le permitan al lector establecer esas relaciones, o el maestro que lo propone sea consciente de esta particularidad del enunciado.

Se encuentran, entonces, dos tipos de enunciaciones en lengua natural que llevarán a una comprensión distinta en la relación que hay entre los años establecidos y los transcurridos. Esto se puede observar en la tabla 1:

Tabla 1. Expresiones en lengua natural que establecen relaciones entre los años transcurridos

Expresión en lengua natural del enunciado del problema 1	t
“Utilice esta función para calcular la tasa de mortalidad infantil en Estados Unidos en a) ”	t = 10 años
b)	t = 45 años

En el enunciado de la figura 10 no se presenta una correspondencia semántica entre los elementos significantes en U1 y U2 que se requieren para el tratamiento numérico que se debe realizar en P1 y P2 porque la representación simbólica algebraica dada se encuentra en términos de t en número de años, y en las preguntas P1 y P2 el autor lo expresa en años transcurridos.

Sobre la congruencia en la organización de la redacción del enunciado, se puede afirmar que la presentación redaccional de éste, como se viene analizando, implica que el lector debe establecer relaciones intermediarias. Esto con el fin de responder a las preguntas del enunciado, pero se podría decir que no hay una correspondencia semántica entre los elementos significantes identificados en el enunciado y aquellos que se requieren para el tratamiento aritmético que hay que efectuar.

Análisis del enunciado del problema 2: exámenes

El enunciado que se presenta en la figura 11 se encuentra en el registro de representación de la lengua natural, y se acompaña de un registro simbólico algebraico auxiliar para representar el modelo matemático logarítmico que relaciona la calificación promedio en un examen y el número de horas dedicadas a estudiar.

Figura 11. Presentación del enunciado del problema 2 (exámenes)

Fuente: tomado de Ángel (2004, p. 644).

En la figura 12 se presentan las posibles unidades segmentadas que relacionan información dada por el enunciado y la articulación con la pregunta formulada; además, se resaltan con rojo las marcas lingüísticas que establecen un significado con las unidades textuales de información en el enunciado del problema.

Figura 12. Segmentación de unidades textuales de la información dada en el enunciado del problema 2 (exámenes)

Fuente: Goyes (2021, p. 96).

A nivel lingüístico, la pregunta formulada en P1 y P2 tiene un nexo lógico con las unidades de información en U1 y U2. La unidad de información en U1 está articulada con la condición dada en U2 porque se explicita la relación entre las variables dependiente e independiente. En este caso, la calificación promedio depende del número de horas dedicadas para presentar un examen. En U2 se expresa que la variable representa el número de horas dedicadas a estudiar, mientras que f(x) corresponde a la calificación promedio de un estudiante. Estas dos relaciones U1 y U2 son necesarias en el enunciado, con el fin de realizar los posibles tratamientos numéricos para dar respuesta a las preguntas formuladas en P1 y P2. Ahora bien, cabe preguntarse acerca del enunciado: ¿a qué se refiere el autor del enunciado con la calificación promedio en puntos?, ¿será acaso que entre más horas de estudio dedique, mayor calificación se puede obtener?, y, en caso contrario, al dedicar menos horas de estudio, ¿la calificación promedio será menor?

En la figura 13 se explicitan posibles presuposiciones que se pueden generar de las diferentes segmentaciones del enunciado del problema 2 (exámenes).

Figura 13. Algunas presuposiciones involucradas en las unidades segmentadas del
enunciado del problema 2 (exámenes)

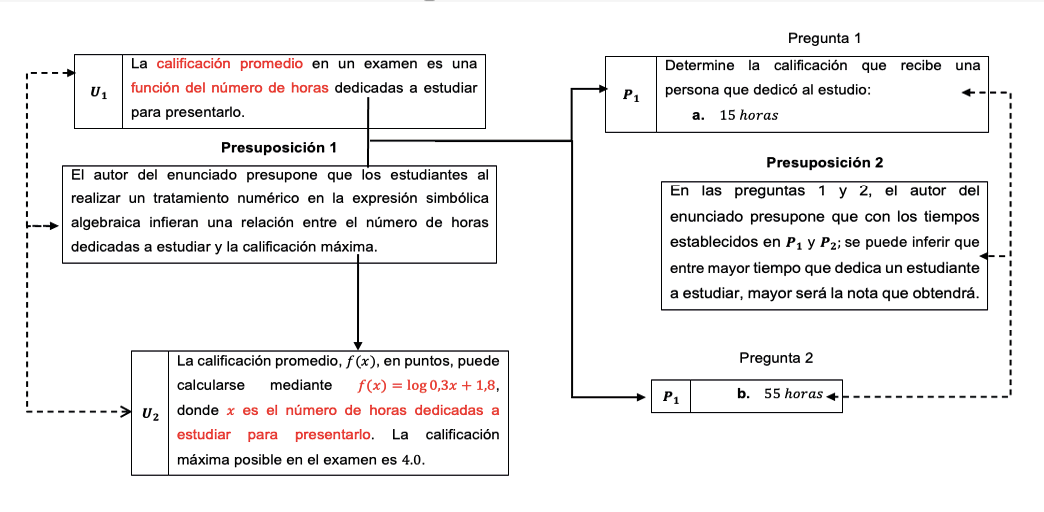
Fuente: Goyes (2021, p. 97).

En este enunciado del problema se pueden identificar unidades de información que afirman algo. Por un lado, la modelación matemática de la función logarítmica de la situación, la calificación máxima posible que se puede obtener y el número de horas de estudio. Por otro lado, aquellas que permiten reconocer la relación entre las unidades de información que afirman algo y lo que se le pide en la pregunta directa o indirecta del enunciado del problema; en este caso, sería determinar la calificación que recibe una persona dependiendo del número de horas que se ha dedicado al estudio.

En estas unidades de información se identifica una marca lingüística como: “la calificación promedio en un examen es una función del número de horas…”, indicando la relación de dependencia entre la calificación promedio y el número de horas, intentando movilizar elementos de relación de dependencia entre variables, es decir, el número de horas (variable independiente) y la calificación promedio (variable dependiente).

En el contenido semántico del enunciado del problema, el autor presupone que con los tiempos establecidos en P1 y P2, el lector puede inferir que entre mayor tiempo se dedica a estudiar, mayor será su nota. Aunque este tipo de interpretación no es posible con la representación de la función f (x) = log 0.3x + 1.8 dada en el enunciado del problema. Esto obedece a que el coeficiente conformado en la representación de la función impacta en el crecimiento de las imágenes de f (x).

Reorganización redaccional de los enunciados de problemas seleccionados de la función logarítmica

Al hablar de reorganización redaccional de los enunciados de problemas, se refiere a la modificación que se efectuó a los enunciados de problemas que se tenían inicialmente. A los cuatros enunciados de problemas seleccionados de la función logarítmica se les realizaron las respectivas variaciones en la redacción del cómo se presentan los enunciados de problemas, representaciones auxiliares, modificaciones en las preguntas que se formulan, las marcas lingüísticas, las variables categoriales y visuales como elementos determinantes para la comprensión del enunciado del problema, con el fin de identificar el papel que cumplen éstas en la comprensión de dichos enunciados.

Posteriormente, se llevó a cabo la implementación de la aplicación de los enunciados de problemas de la función logarítmica a un grupo de siete estudiantes de una institución universitaria de educación superior en el año 2020; participaron cuatro hombres y tres mujeres que estaban inscritos en el curso de matemáticas básicas que ofrece dicha universidad.

A continuación, se presentan dichas modificaciones a los enunciados de problemas seleccionados.

Reorganización redaccional en el enunciado del problema 1: tasa de mortalidad infantil

En el enunciado del problema 1 se realizó una contextualización del significado de la mortalidad infantil, cuyo propósito es que el lector se ubique y pueda identificar la connotación de la palabra “mortalidad” de la situación propuesta en el problema. Además, se presenta al lector el registro gráfico cartesiano que modela el enunciado propuesto (véase la figura 14).

Figura 14. Representación gráfica cartesiana del enunciado del problema 1: tasa de mortalidad infantil

Fuente: Goyes (2021, p. 110).

En la figura 14 se resalta en el eje x la correspondencia entre t años y los años que transcurren, es decir, que 1960 corresponde a 0 años, y así sucesivamente.

La primera pregunta propuesta se encuentra en términos de analizar la situación planteada y su representación gráfica cartesiana: ¿cuál es la tasa de mortalidad infantil en 1960? Se busca que los estudiantes identifiquen, de acuerdo con la situación planteada y su representación gráfica cartesiana, la tasa de mortalidad infantil en el año 1960. De modo que estos realicen los tratamientos aritméticos adecuados para responder a la pregunta del problema propuesto. Posterior a ello, se plantea la pregunta de visualizar en la representación gráfica cartesiana la diferencia entre la tasa de mortalidad infantil entre los años y para identificar que hay un descenso en el número de muertes infantiles.

En distintos ítems del enunciado del problema se propone que “si la función que modela el número de muertes infantiles con respecto al número de años es esta otra representación: f(t)=26+12,1 log(t+1), , ¿cómo crees que sería su representación gráfica cartesiana?”, con la finalidad que los estudiantes puedan identificar y relacionar las variables categoriales en la representación simbólica algebraica con las visuales de la representación gráfica cartesiana. Para ello, el estudiante debe reconocer dichas variaciones (desplazamientos, asíntotas, etc.) en las variables categoriales y cómo estas inciden o afectan los valores visuales, o viceversa.

Finalmente, se propone a los estudiantes que relacionen la representación simbólica algebraica de una función logarítmica con su respectiva representación gráfica cartesiana. Ese enunciado del problema se plantea en los siguientes términos: “A partir del año 1960, la función que modela la tasa de disminución de mortalidad infantil en nuestro país se expresa de la siguiente manera, f(t)=14-6.5 log(t+1); en el que t es el número de años. En cada una de las siguientes opciones, justifique por qué corresponde o no a la modelación simbólica algebraica planteada”.

Con esto se esperaba que los estudiantes realizaran sus justificaciones a partir de las variables visuales como cortes con los ejes x e y, desplazamientos horizontales o verticales, entre otros, que hacen parte de las características propias de la función logarítmica.

Reorganización redaccional en el enunciado del problema 2: exámenes

En el enunciado del problema 2 se realizó una modificación en las variaciones de la redacción, identificando las marcas lingüísticas de la variable dependiente e independiente. Esto se puede observar cuando en el enunciado propuesto se menciona que “el número de horas dedicadas a estudiar para presentar el examen y la calificación que puede obtener un estudiante corresponde a f(x)”. De igual modo, se presenta al lector la representación gráfica cartesiana que modeliza el enunciado propuesto.

Luego, se les plantean a los estudiantes dos representaciones gráficas cartesianas con su correspondiente representación simbólica algebraica de la función, que modelan la situación problema de la calificación que puede obtener un estudiante cuando dedica un cierto número de horas a estudiar, en el que la variable en las funciones dadas representa el número de horas dedicadas a estudiar para presentar el examen. Las modelaciones de las funciones que describe la situación son las siguientes f(x) = log 0.3x + 1.8 y g(x) = log(2x)+2.

Esto quiere decir que la representación gráfica cartesiana de la función g(x) = log(2x)+2 proviene de sumar 2 a cada imagen de la función básica de logx y como la base del logaritmo a > 1; se observa que para x > 1 aumentan los valores lentamente, mientras que la representación gráfica cartesiana de g(x) tendrá el mismo bosquejo de la curva de la función f(x) = log 0.3x + 1.8, pero se han desplazado dos unidades verticales hacia arriba, y el crecimiento de los puntos coordenados en el plano cartesiano es lento.

Con esto se buscó que los estudiantes realizaran un análisis de la representación simbólica algebraica y la gráfica cartesiana, de modo que lograran articular tanto las variables categoriales como las variables visuales de los respectivos registros semióticos (simbólico algebraico y gráfico cartesiano) necesarios para el proceso de comprensión de los enunciados de problemas.

En uno de los ítems del enunciado se presentó una nueva representación simbólica algebraica de la función, en la cual la representación de dicha función estaba constituida por un signo negativo que antecede en ±b; los estudiantes analizaron e interpretaron cómo éste incidía o afectaba los puntos coordenados en la representación gráfica cartesiana.

Resultados de la implementación de los enunciados de problemas reorganizados redaccionalmente sobre la función logarítmica

En el enunciado del problema 1 se buscó que los estudiantes, a partir de la representación simbólica algebraica de una función dada, realicen la conversión a la representación gráfica cartesiana. Para esto, los estudiantes pudieron identificar algunas variables categoriales en la representación simbólica de la función dada, y se articularon con algunas variables visuales en la representación gráfica cartesiana. En las producciones de los estudiantes se observó que la mayoría de ellos realizaron primero un boceto del gráfico cartesiano que se articula con la representación simbólica algebraica de la función trabajada. En éstas, utilizaron variables de significado como cortes con los ejes, asíntotas, crecimiento, etc., y aprehensiones globales cualitativas de las variables visuales en la representación gráfica cartesiana de la función logarítmica.

En la figura 15 se puede observar que frente a la pregunta del problema: ¿cómo crees que sería la representación gráfica cartesiana de la función f(t) = 26 + 12,1 log(t + 1)?, en la producción escrita del estudiante, se observó que utiliza una representación auxiliar como la gráfica cartesiana de la función logarítmica básica f(x) = log(x) para hacer un análisis comparativo entre las representaciones de la función básica logarítmica y la función dada en el enunciado, haciendo uso de las transformaciones (tratamientos) que implican desplazamientos, aberturas, entre otras.

Enunciado del problema 1: T2p651-75TMI (tasa de mortalidad infantil)

Registro simbólico algebraico-gráfico cartesiano

Figura 15. Respuestas de las producciones representativas de un estudiante

Fuente: Goyes (2021, p. 122).

En la parte izquierda de la figura 15 (véase el recuadro verde), el estudiante 7 ubica en el plano cartesiano la curva que describe el comportamiento de la función logarítmica básica, señalando con una flecha el corte con el eje X, identificando que la pareja ordenada en ese corte es 0,26. El valor visual del punto de corte (0.26) es importante, dado que indica que el estudiante está tomando en cuenta el contexto extramatemático que se vinculó en la reorganización redaccional del enunciado (tasa de mortalidad). Esto se hace un poco más evidente cuando menciona que es “creciente en todo su dominio”. Además, indica que la asíntota verticual es x = 0 en la función logarítmica básica, y el trazo de la curva que realiza sobre el plano cartesiano se desplaza continua e infinitamente sobre la asíntota y luego va creciendo.

Se puede observar en la producción del estudiante 7 que su proceso va más allá de lo que se solicita en la pregunta formulada del enunciado, porque cuando representa los gráficos cartesianos de la función logarítmica básica y la modelación de la función del enunciado del problema, está haciendo un análisis de las posibles transformaciones en el interior del registro gráfico cartesiano que tiene la representación de la función logarítmica básica f(x) = logx en la representación f(t) = 26 + 12,1 log(t + 1). Con esto se observa que el estudiante 7 logra avanzar en la articulación de los registros gráficos cartesianos y de escritura simbólica algebraica acudiendo al registro de lengua natural para explicar los cambios tanto visuales como categoriales de la función dada. En resumen, el reconocer los cambios tanto visuales como categoriales, se logra asignar correctamente en la representación simbólica algebraica de la función un cambio visual en la representación gráfica cartesiana, es decir, un desplazamiento del gráfico cartesiano hacia la derecha o izquierda, asociados a los coeficientes 26 y 12,1 y sus símbolos positivos en la representación algebraica f(t) = 26 + 12,1 log (t + 1) del enunciado problema propuesto.

En la producción del estudiante 1, realiza la figura forma de la representación gráfica cartesiana de la función f(t) = 26 + 12,1 log (t + 1) en el plano coordenado a escala de 5 en 5 y, además, representa en el plano cartesiano otras parejas ordenadas dando a entender que la curva logarítmica de la función es continua.

Figura 16. Respuestas de las producciones representativas de un estudiante

Fuente: Goyes (2021, p. 125).

En la figura 16 se puede observar que el estudiante 1, aunque no realiza la representación gráfica cartesiana de la función logarítmica básica, expresa este hecho en las unidades discursivas en lengua natural mencionando que “su representación gráfica sería la mostrada, se saca de una función básica logarítmica, en esta aumentaría la tasa de mortalidad, sería cóncava hacia abajo”. Esto significa que el estudiante 1 ha visualizado la representación de la función logarítmica básica identificando variables visuales en el comportamiento de dicha función, en articulación con la representación simbólica algebraica f(t) = 26 + 12,1 log (t + 1) para asignarle el desplazamiento en tantas unidades hacia la izquierda; determinar cortes y reflexiones sobre el eje x; concavidades, entre otras, y así mismo le asignó características en el comportamiento de la representación gráfica cartesiana de la función dada en el enunciado problema propuesto.

La anterior descripción de la producción escrita hecha por el estudiante 1 evidencia la importancia que tuvo la modificación de la variable visual del signo en la representación de la función, dado que en el enunciado del problema original tenía un signo negativo y en la variación redaccional se cambió a positivo. Este cambio le posibilitó un análisis para identificar que el número de muertes iba a crecer, y esto le impacta su representación gráfica cartesiana porque la curva crece a medida que avanza el tiempo.

Por lo tanto, puede afirmarse que el estudiante 1 logra articular las variables categoriales de la representación simbólica algebraica con las variables visuales de la representación gráfica cartesiana de la función logarítmica. Esto se evidencia cuando el estudiante encuentra una representación gráfica cartesiana como la función logarítmica básica, que le permite organizar la información del enunciado problema propuesto con la representación de la función f(t) = 26 + 12,1 log (t + 1) , y de esta forma logró realizar su representación gráfica cartesiana.

En el enunciado del problema 1 se buscaba que los estudiantes relacionaran la representación simbólica algebraica de la función f(t) = 14 - 6,5 log(t + 1) con su respectiva representación gráfica cartesiana. Se espera, entonces, que los estudiantes justifiquen su elección de acuerdo a los desplazamientos, cortes con los ejes, asíntotas, etc. Por ejemplo, que en la variable categorial de la representación simbólica algebraica f(t) = 14 - 6,5 log(t + 1), el coeficiente 14 representa la ordenada en el punto de corte con el eje y, o que el signo negativo conformado en el coeficiente indica que la función logarítmica es decreciente en todo su dominio.

De acuerdo con las tablas 2 y 3, se evidencia que en las producciones de la mayoría de los estudiantes, para identificar la asociación de la representación gráfica cartesiana con su correspondiente simbólica algebraica, utilizaban los términos propios de la función logarítmica, tales como cortes con el eje, crecimientos, decrecimientos, etc., para explicar o justificar por qué correspondería o no a la modelación simbólica algebraica planteada.

Tabla 2. Producciones de los estudiantes a la solución del enunciado del problema 1

Estudiante 1
Estudiante 2

Tabla 3. Producciones de los estudiantes a la solución del enunciado del problema 1

Estudiante 7
Estudiante 3

En las tablas 2 y 3 se puede observar que los estudiantes, en las unidades discursivas, recurren a marcas lingüísticas que aluden a la función logarítmica como tasa de disminución, aumento, una disminución, dominio, decreciente, creciente, cortes con y, una reflexión en el eje x, signo (-) de la función, entre otros, que son palabras para referenciar la variación de una magnitud con respecto a otra, sobre las cuales hay una dependencia o correlación. Algunas de esas marcas se han presentado en el enunciado problema, de manera que se mantiene una correspondencia entre lo conceptual y operatorio de la función logarítmica.

El uso de estas marcas lingüísticas por parte de los estudiantes está directamente movilizado por el cambio en la representación de la función que se realizó al enunciado original porque este cambio provocó la necesidad de ir visualizando en las representaciones gráficas cartesianas si la curva es cóncava hacia arriba o hacia abajo, lo cual expresaron en las marcas lingüísticas que utilizaron. Esto es muy importante para el proceso de comprensión del problema porque les permitió a los estudiantes entender si la tasa de mortalidad crece o decrece.

En el enunciado del problema 2 (exámenes), que solicitaba a los estudiantes hacer un análisis de la representación simbólica algebraica y la representación gráfica cartesiana de la función f(x) = log 0.3x + 1.8 y g(x) = log (2x) + 2, identificando los elementos comunes y no comunes entre las representaciones simbólicas algebraicas y gráficas cartesianas, con el objeto de explicitar las correspondencias entre variables categoriales y visuales, se observó que los estudiantes lograron establecer la correspondencia entre las unidades categoriales presentadas en el enunciado del problema con la representación gráfica cartesiana. Es decir, que los estudiantes tuvieron acercamiento a cómo el cambio en los valores categoriales de la función logarítmica presentada en el enunciado genera o afecta una variación en la representación gráfica cartesiana correspondiente.

En la tabla 4 se muestran las respuestas desarrolladas por algunos estudiantes que participaron en la investigación, para identificar semejanzas y diferencias, tanto en las representaciones gráficas cartesianas como en las simbólicas algebraicas.

Tabla 4. Respuestas dadas por los estudiantes frente al enunciado del problema 2

Semejanzas

Diferencias

Las dos representaciones gráficas de f(x)= log10 (0,3x) + 1,8 y g(x) = log10 (2x) + 2 tienen un comportamiento creciente. Las dos representaciones gráficas de f(x)= log10 (0,3x) + 1,8 y g(x) = log10 (2x) + 2 son cóncavas hacia abajo. Las dos representaciones gráficas de f(x)= log10 (0,3x) + 1,8 y g(x) = log10 (2x) + 2 tienen como base el número 10 y por eso, la forma de su crecimiento es idéntica. Claro está que con diferentes valores. El dominio y rango de las funciones es el mismo. La asíntota vertical en ambas funciones es x = 0

La función g(x) = log10 (2x) + 2 por propiedad de desplazamiento y traslación de funciones sube 2 unidades verticalmente. En la función f(x)= log10 (0,3x) + 1,8. Si el número que acompaña a la x, es menor que 1, su corte se aleja de cero cada vez más. La gráfica se traslada 1,8 unidades hacia arriba. En la función g(x) = log10 (2x) + 2. Si el número que acompaña a la x, es mayor que 1, su corte tiende a cero. La gráfica se traslada 2 unidades hacia arriba.

Las respuestas de la tabla 4 muestran que los estudiantes logran identificar la variable visual del comportamiento referido al crecimiento de las notas que puede obtener un estudiante. Para ello, visualizan la representación gráfica cartesiana de la función dada y le hacen corresponder la variable simbólica log(ax) indicando que si a > 1, su corte se acerca a cero. Otra de las variables visuales que identifican los estudiantes es el desplazamiento de unidades hacia arriba en el eje y, articulándola con la identificación del signo y los coeficientes que se conforman en las representaciones simbólicas algebraicas de las funciones dadas. El valor visual sobre las asíntotas de ambas funciones se evidencia cuando mencionan que “el número que acompaña a x, es mayor que 1, su corte tiende a cero”; quiere decir que hacen corresponder la variable simbólica en log(ax) para determinar que la asíntota es x = 0.

Los anteriores análisis de los estudiantes emergen de las variaciones redaccionales que se hicieron al enunciado del problema original. Esas variaciones fueron la elaboración de las representaciones gráficas cartesianas con sus correspondientes representaciones simbólicas algebraicas para visualizar el comportamiento de las notas promedio de los estudiantes. En una de las representaciones, el coeficiente que acompaña a log(ax) es una cantidad entera, y en la otra no, por lo cual el crecimiento de la representación de la función no es el mismo.

En la figura 17 se presentan dos producciones de los estudiantes 1 y 6, respectivamente, donde se evidencia una lectura de las representaciones gráficas cartesianas dadas en el enunciado, que comprende una interpretación global de las funciones logarítmicas, dado que se discriminan las variables visuales en correspondencia con las variaciones en los símbolos de la representación simbólica algebraica.

Figura 17. Respuestas de las producciones representativas de los estudiantes 1 y 6

Fuente: Goyes (2021, pp. 141-142).

Con las siguientes unidades de información realizadas por los estudiantes: “y = log (2x) + 2 si el número que acompaña la x es mayor que 1, x > 1”; “y = 1.8 si el número x < 1 su corte se aleja del 0 cada vez más”; “ambas son crecientes”; “una misma concavidad”; “el dominio es igual x ε (0,∞)", ellos establecen correspondencia con las variaciones en el registro simbólico algebraico.

Figura 18. El discurso presente en las producciones de los estudiantes, centrándose en la interacción entre los sistemas semióticos gráficos cartesianos y los simbólicos algebraicos de la función f(x) = log 0.3x + 1.8

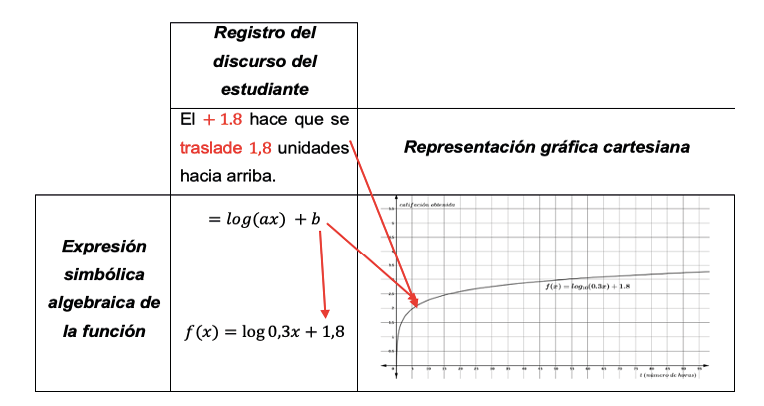
Fuente: Goyes (2021, p. 143).

En la figura 18 se analizan las variables visuales que los estudiantes discriminan en la representación gráfica cartesiana y las articulan con las variaciones en los símbolos de la representación simbólica algebraica.

Como se muestra en las figura 18, cuando los estudiantes mencionan que “el + 1.8 hace que se traslade 1,8 unidades hacia arriba” y “ + 2 se traslada 2 unidades hacia arriba”, están identificando en la variable categorial de forma general en la representación de la función y = log (ax) +b, en el cual b indica los desplazamientos que tienen las imágenes en el plano cartesiano (esto se puede observar en las flechas rojas que se marcan en la figura 18.

Así mismo, se ilustran las enunciaciones discursivas por parte de los estudiantes, indicando que a cada unidad significante elemental en el registro de partida (simbólica algebraica) le corresponde una única unidad significante elemental en el registro de llegada (gráfico cartesiano). Es decir, que la información que describen ambos estudiantes en lengua natural se corresponde con los valores tanto visuales como categoriales que identifican en el enunciado del problema propuesto porque expresan las unidades significantes como los desplazamientos, cortes, crecimientos y asíntotas que dan cuenta del reconocimiento de las variables visuales en la representación gráfica cartesiana y de sus relaciones de covariación.

En el enunciado del problema 2 (exámenes), los estudiantes logran identificar las unidades significantes de éste en el registro de lengua natural, esto es: la variable independiente (el tiempo) y dependiente (el promedio de calificaciones), como también la relación que guardan los valores (parejas en el plano coordenado) de dichas variables y su representación gráfica cartesiana. Dichas variaciones se inscribieron en el mismo contexto extramatemático del problema original, el cual resulta ser más cercano a los estudiantes, y con ello, más probable de ser comprendido. En consecuencia, los estudiantes pueden empezar a interpretar que, debido al comportamiento de los puntos coordenados en las representaciones gráficas cartesianas, no se pueden obtener resultados acordes a un buen promedio en las notas porque cada vez necesitarían más tiempo para estudiar.

Conclusiones

Los elementos teóricos propuestos en la perspectiva semiótico-cognitiva, desarrollada por Duval (1988a, 1988b, 1999, 2004, 2006, 2017) y los aportes de la teoría semiótica-cognitiva y lingüística planteada por Pontón (2008, 2012) brindan a los maestros e investigadores fundamentos que permiten un acercamiento a todo lo que implica el proceso de comprensión de un enunciado de problema matemático, y su aprendizaje. Estos elementos resultan ser necesarios para que el maestro pueda analizar los enunciados que se proponen “usualmente” en los textos escolares, hacer la selección de estos enunciados y examinar una reorganización redaccional que permita llevar a los estudiantes a construir una comprensión del enunciado o un acercamiento a esta comprensión, que aprendan intencionalmente a establecer las relaciones entre variables lingüísticas con las variables categoriales, y después, su relación con variables visuales, que generen procesos de conversión para la solución de los problemas.

Un primer elemento teórico que se reafirmó se refiere a los procesos cognitivos y semióticos involucrados en el pensamiento matemático, con lo cual es posible concluir que toda actividad matemática debe involucrar actividades que lleven a los estudiantes a distinguir dos clases de transformaciones semióticas: la conversión y el tratamiento. Es decir, se hace primordial que en las actividades que se propongan vinculen estas operaciones cognitivas. Estas posturas teóricas se corroboraron en las producciones de los estudiantes analizadas en el trabajo investigativo, dado que se observó que, al solicitarles interpretar una representación simbólica algebraica con respecto al enunciado del problema propuesto, ellos recurrieron a una representación auxiliar como la gráfica cartesiana de la función logarítmica básica, analizando las posibles transformaciones del registro simbólico algebraico y articulando tanto las variables categoriales como las variables visuales de los respectivos registros semióticos (simbólico algebraico y gráfico cartesiano). También se evidencia que los estudiantes logran avanzar en la articulación de los registros gráficos cartesianos y de escritura simbólica algebraica acudiendo al registro de lengua natural para explicar los cambios tanto visuales como de las variables categoriales simbólicas de la función dada.

Un segundo elemento teórico que se logra identificar en esta investigación está relacionado con la construcción de un acercamiento a la comprensión del objeto matemático, a partir de la articulación entre registros de representación semiótica, el cual requiere el reconocimiento del objeto matemático común entre dos representaciones de contenidos diferentes. En referencia a este segundo elemento, como un resultado de la investigación se observó que los estudiantes logran visualizar en la representación simbólica de la función y = log(ax) correspondencias con las variables categoriales de la función f(t) = a - blog (ct + d), que les permite explicar algunos de los desplazamientos de las unidades hacia arriba en el eje y, así como identificar el signo en la representación simbólica algebraica para reconocer crecimientos o decrecimientos de la función logarítmica dada.

También se puede concluir que las organizaciones redaccionales de los enunciados de problemas son determinantes para promover la articulación de los registros de representación semiótica, que emplean los estudiantes al dar soluciones a las preguntas que se les propongan. En los procesos de los estudiantes se evidencian articulaciones de distintos registros de representación semiótica. Describieron características propias de la función logarítmica, visualizaron el comportamiento de la función logarítmica en correspondencia con las variables categoriales de la representación simbólica algebraica, establecieron correspondencias entre los elementos presentados en el enunciado del problema con la representación gráfica cartesiana o simbólica algebraica, entre otros.

Al realizar las modificaciones redaccionales a los problemas representantes del campo seleccionados y presentarlas a los estudiantes, se observó que los estudiantes lograron identificar y articular las variables visuales del registro gráfico cartesiano con las variables categoriales de las representaciones simbólicas algebraicas. Por ejemplo, al vincular una representación gráfica cartesiana a cada enunciado problema y cambiar en las variaciones categoriales de las funciones logarítmicas, los estudiantes realizaron los tratamientos adecuados y necesarios en cada registro semiótico de representación para organizar la información en el enunciado del problema propuesto. De este modo, los estudiantes reconocieron los desplazamientos en tantas unidades hacia la izquierda o derecha teniendo de referencia la función básica logarítmica; así mismo, determinaron cortes con los ejes cartesianos y reflexiones sobre el eje x, concavidades, entre otras características de la función. Otra variación redaccional implementada estuvo relacionada con las marcas lingüísticas presentes en los enunciados de problemas seleccionados. Por ejemplo, al enunciado del problema 1, cuyo contexto está relacionado con la tasa de mortalidad infantil, se le realizó una variación redaccional que permitiera ampliar el significado de la palabra “mortalidad” en la situación problema propuesta. Con esta variación, los estudiantes pudieron organizar las unidades de segmentación de la información del enunciado para responder a las preguntas formuladas. Igualmente, discriminaron las unidades significantes de las variables, tanto categoriales como visuales, y al hacerlas corresponder con otras representaciones semióticas, efectuaron el tratamiento adecuado contribuyendo al proceso de comprensión del enunciado.

Por ejemplo, en la figura 19 se puede observar que el estudiante 1, aunque no realizó la representación gráfica cartesiana de la función logarítmica básica, expresa este hecho en las unidades discursivas en lengua natural mencionando que “su representación gráfica sería la mostrada, se saca de una función básica logarítmica, en esta aumentaría la tasa de mortalidad, sería cóncava hacia abajo”. Esto significa que el estudiante 1 logró identificar la asociación de la representación gráfica cartesiana con su correspondiente representación simbólica algebraica, utilizando los términos en el marco de las marcas y relaciones propias de la función logarítmica, tales como cortes con el eje, crecimientos, decrecimientos, etc., para explicar o justificar la representación gráfica cartesiana con la modelación simbólica algebraica planteada.

Figura 19. Respuestas de las producciones representativas del estudiante 1

Fuente: Goyes (2021, p. 150).

En la figura 19 se pudo observar la importancia que tuvo la modificación de la variable visual del signo en la representación simbólica algebraica de la función, dado que en el enunciado del problema original tenía un signo negativo y en la variación redaccional se cambió a positivo. Este cambio le posibilitó al estudiante 1 afirmar que el número de muertes iba a crecer y, por ende, su representación gráfica cartesiana sería cóncava hacia abajo. Se puede afirmar que las modificaciones redaccionales realizadas a los enunciados de problemas posibilitaron que los estudiantes articularan las representaciones gráficas cartesianas con nuevas modelaciones simbólicas algebraicas, a través de una interpretación global del registro cartesiano, que les ayudó a identificar y relacionar elementos que no cambian. Es decir, que visualizaron las características de esta representación para deducir el impacto al modificar una variable categorial simbólica algebraica.

En ese sentido, una recomendación para los maestros en ejercicio es acercarse a estos elementos teóricos que permitan un análisis de los enunciados, que consideren la reflexión sobre reorganización de los enunciados que genere articulación entre distintos registros de representación semiótica, lo cual permitirá construir una comprensión de éstos teniendo la consciencia de que esta comprensión no se da de manera natural ni espontánea. Del mismo modo, tener en cuenta que cuando se proponga cualquier enunciado de problema a los estudiantes, se debe con anticipación reflexionar y repensarse las organizaciones redaccionales, con el fin de propiciar operaciones cognitivas, tales como la conversión y el tratamiento, que son fundamentales en la comprensión y resolución de éstos.

Referencias

Ángel, A. (2004). Álgebra intermedia. México: Pearson Educación.

Duval, R. (1988a). Gráficas y ecuaciones. La articulación de dos registros. México: Antología En Educación Matemática Cinvestav.

Duval, R. (1988b). Las representaciones gráficas: funcionamiento y condiciones de su aprendizaje. Estrasburgo: IREM.

Duval, R. (1999). Semiosis y pensamiento humano. Registros semióticos y aprendizaje intelectuales. Traducción realizada por Myriam Vega Restrepo, (1ª ed.). Cali: Artes Gráficas Univalle.

Duval, R. (2004). Los problemas fundamentales en el aprendizaje de las matemáticas y las formas superiores del desarrollo cognitivo. Bogotá: Editorial Universidad Distrital Francisco José de Caldas.

Duval, R. (2006). Un tema crucial en la educación matemática: La habilidad para cambiar el registro de representación. La Gaceta de la Real Sociedad Matemática Española, 9, 143-168.

Duval, R., & Sáenz-Ludlow, A. (2016). Comprensión y aprendizaje en matemáticas: perspectivas semióticas seleccionadas. Universidad Distrital Francisco José de Caldas.

Duval, R. (2017). Semiosis y pensamiento humano. Registros semióticos y aprendizaje intelectuales. Traducción realizada por Myriam Vega Restrepo, (2ª ed.). Cali: Artes Gráficas Univalle.

Goyes, N. (2021). La comprensión de los enunciados de problemas de la función logarítmica a partir de una mirada semiótica cognitiva. Cali: Universidad Nacional de Colombia. Guzmán Retamal, I. (1998). Registros de representación, el aprendizaje de nociones relativas a funciones: voces de estudiantes. Revista latinoamericana de investigación en Matemática Educativa., 1, 5-21. https://repositorio.unal. edu.co/handle/unal/81147

National Council of Teachers of Mathematics (NCTM). (2000). Principles and Standards for School Mathematics. Reston, VA: National Council of Teachers of Mathematics.

Martínez, M. M. (2014). La investigación cualitativa (sintesís conceptual). Revista de Investigación En Psicología, 9(1), https://doi.org/10.15381/rinvp.v9i1.4033.

MEN. (2006). Estándares Básicos de Competencias. Bogotá.

Ministerio de Educación Nacional (MEN). (1998). En Lineamientos Curriculares.

Planchart, O. (2002). La visualización y la modelación en la adquisición del concepto de función. Cuernavaca: Universidad Autónoma del Estado de Morelos. Tesis doctoral inédita.

Pontón, T. (2008). Una propuesta multirregistro para la conceptualización inicial de las fracciones.

Pontón, T. (2012). La comprensión de enunciados de problemas en la enseñanza y el aprendizaje inicial de los números racionales.

.........................................................................................................................................................

Nelson Javier Goyes Bastidas

Magíster en Enseñanza de las Ciencias Naturales y Exactas. Egresado de la Maestría en Enseñanza de las

Ciencias Exactas y Naturales, Universidad Nacional de Colombia, Palmira, Colombia. Sus temas de interés se centran en Educación Matemática, las dificultades en la comprensión y aprendizaje de las matemáticas y la transformación educativa y pedagógica. Publicaciones recientes: Goyes Bastidas, N. (2021). La comprensión de los enunciados de problemas de la función logarítmica a partir de una mirada semiótica cognitiva. Universidad Nacional de Colombia. https://repositorio.unal.edu.co/handle/unal/81147. Saavedra Urrego, E., Valencia Becerra, J., & Goyes Bastidas, N. (2011). Análisis y caracterización de la gestión didáctica del docente en una secuencia didáctica sobre la continuidad y límite, desde la teoría de situaciones didácticas. Voces Y Silencios. Revista Latinoamericana De Educación, 2(especial), 65–77. https://doi.org/10.18175/vys2.especial.2011.04

Teresa Pontón Ladino

Docente Asistente. Universidad Nacional de Colombia. Coordinadora de postgrado FIA y de Maestría en enseñanza de las ciencias exactas y Naturales. Sus temas de interés se centran en Didáctica de las matemáticas, Formación de maestros y Educación Matemática. Obando-Zapata, G., Pontón-Ladino, T., Parada-Rico, S & Villa-Ochoa, J. (2020) Research into cognition and numerical thinking in Colombia (Investigación sobre cognición y pensamiento numérico en Colombia), Studies in Psychology, 41:2, 319-347, DOI: 10.1080/02109395.2020.1748841 Pontón Ladino, T., & Lourido Guerrero, D. M. (2021). Una propuesta multirregistro para la enseñanza de los números irracionales. UNIÓN - REVISTA IBEROAMERICANA DE EDUCACIÓN MATEMÁTICA, 17(61). Recuperado a partir de https://union.fespm.es/index.php/UNION/article/view/195

---